条件概率的和(条件概率与概率这两个概念的区别与联系)

导语：「概率论与数理统计」今天来谈谈条件概率和联合概率的定义

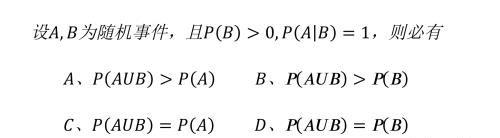
最近在复习考研数学中的概率论与数理统计，其中有很多定义，今天结合题目打算来讲一下条件概率和联合概率的定义和用法。

概率，从英文上来说是Probability，也就是说，我们一般可以用P(X)来代替，就说X的概率是P(X)。

联合概率

联合概率的定义是多个随机变量分别满足各自条件的概率，准确点来说就是两者都会发生的概率。

那很明显，就是两个随机变量发生概率的交集，一般我们可以用P(MN)或者P(M∩N)来表示。

延伸：那么，有交集肯定会有并集，交集说的是两者共同发生的概率，那么并集就是除了两者共同发生的概率外的其他概率。

由此可得：P(MUN)=P(M)+P(N)-P(M∩N)

条件概率

条件概率的定义为某个事件在另一个事件已经发生下的概率。

假设某个事件为M，另一个事件为N，那么在另一个事件已经发生下的概率，可以知道，在M事件发生的时候，N事件也要发生，那么就可以说明这个概率便是两者都发生的概率，也就是两个事件的交集。

然后总共的概率就是N事件发生的概率，所以要除以N事件的概率，才会得到条件概率，也就是：

P(MN)/P(N)。

一般是用P(M|N)=P(MN)/P(N)来进行表示的。

如果说无法理解概念的话，完全可以背下来。

好，根据上面两个概念，给出一道实际例题来做一下，如图所示：

这道题告诉我们条件概率是P(A|B)=1，我们由概念可知P(A|B)=P(AB)/P(B)=1。

就可以知道P(AB)=P(B)。

来分析选项，四个选项都是由事件A和事件B同时发生的概率和其他事件单独发生的概率进行比较。

所以，我们只需要得出事件A和事件B同时发生的概率，以及事件A和事件B发生的概率。

由概念可知，P(AUB)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(B)=P(A)

所以完全就能够得到结果，C就是正确答案。

而至于与P(B)进行比较，明显这里无法进行判断。

结果如图所示：

总结：

对于条件概率和联合概率这两种定义而言，记下来或许是最方便的做法，在考研数学中，概率论与数理统计并不是特别难，慢慢做就行，平时复习的时候好好地把概念都记下来。

本文内容由小葵整理编辑！