高中物理杆的平衡问题受力分析图(高中物理杆的受力方向)

导语：高中物理杆的平衡问题受力分析

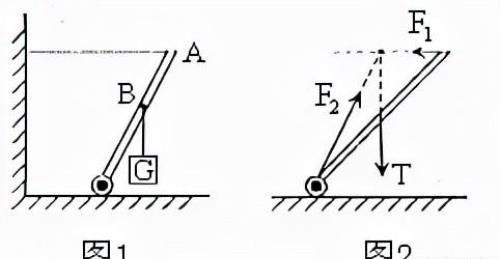
1、轻杆模型的受力问题

在共点力平衡的问题中，常常有“轻绳（绳重不计）、轻杆（杆重不计）及轻弹簧（弹簧质量不计）”的说法，我们要特别注意这些。其中，不少同学对轻杆的施力或受力有误解，认为轻杆所受的力或它施在别的物体上的力一定沿轻杆的方向，但事实并非如此。如图1所示，轻杆的一端可绕O点转动，另一端A拴在一条水平的绳子上，有一重物挂在杆的中点B上。对轻杆受力分析可知，轻杆受到绳拉力F1、竖直绳子的拉力T和地面对它的作用力F2，这三个力形成共点力。从图2可以看出，轻杆两头的受力方向都不沿杆的方向。

判断轻杆所受的力是沿沿杆的方向的方法：

如果轻杆除两端以外不受与杆有夹角的外力的作用。也就是说，对于轻杆，如果只有两端受力，则杆两端所受的一个力（或几个力的合力）的方向必定沿杆的方向。

例1、如图3所示，不计重力的轻杆OP能以O点为圆心在竖直平面内自由转动。P端挂一重物，另用一根轻绳通过滑轮系住端，在F的作用下OP和竖直方向的夹角α缓慢增大时（0<α<π），则两绳对杆的作用力的大小（ ）

A.恒定不变

B.逐渐增大

C.逐渐减小

D.先增大后减小

图3

分析：解答本题，首先应知道轻杆在P点所受的T1、T2的合力一定沿杆的方向，这是解题的关键。在本题中如果合力F不沿轻杆的方向，则轻杆在力F力矩的作用下将发生转动，杆也就不可能处于平衡状态了。

解析：在本题中，轻杆只有两端受力，所以轻杆在P点所受的T1、T2的合力F一定沿杆的方向。如4图所示。

图4

由三角形相似可知：

，可得：

。

即本题的答案为A。

2、非轻质杆的受力及平衡问题

所谓非轻质杆就是杆本身的重力不能忽略。在处理非轻质杆的平衡问题时，一般采用三力汇交原理和力矩的知识进行解答。所谓三力汇交原理就是一个物体如果受三个非平行力作用而处于平衡状态，则这三个力一定作用在物体的同一点或者这三个力的作用线一定相交于同一点。非轻质杆在三个非平行力作用下的平衡问题是共点力平衡的典型模型之一，运用三力汇交原理解决共点力平衡是一种常用的方法。在此必须指出：非轻质杆中的三力不一定就是三个力，而是三个作用点。某些作用于同一点的两个力可以用一个等效力取代。

运用三力汇交原理求解非轻质杆的具体问题时，首先要判断是否属于三个非平行力的平衡问题，这是个难点，也是关键。如果能够做出肯定的判断，就将三个力在不改变各力方向的前提下，移至汇交点，然后再利用平衡条件建立方程求解。

在大量的有关杆在三个力作用下的平衡问题中，最常见的模型是已知两个力，第三个力未知。解决这类问题时，首先应找出已知的两个力的交点，然后根据三力汇交原理做出另一个力的方向，以下的问题就容易解决了。

例2、重力为G的均质杆一端可绕O点转动，另一端拴在一条水平的绳子上，杆与水平面成α角，如图5所示。已知绳中张力大小为T，求O点对杆的作用力。

图5

分析：本题利用三力汇交原理（如图6），很容易地确定出了O点对杆的作用力的方向，使问题变得简单明了。另外本题也可以做出绳子的拉力T、杆的重力G、O点的作用力这三个力的矢量所组成的矢量三角形，利用矢量三角形求解。

图6

解析：取均质杆为研究对象，它受三个力作用，即重力G、绳子拉力T和O点作用力F，受力图如图7所示，因为杆处于平衡状态，所以这三个力的作用线一定相交于同一点。

图7

由图6，运用平衡条件得：

，

。

本文内容由小欣整理编辑！