特征值和特征向量到底是什么(特征值特征向量的定义)

导语：众人皆醉我独醒——深入理解“特征值”和“特征向量”

这是《机器学习中的数学基础》系列的第7篇，也是线性代数的最后一篇。

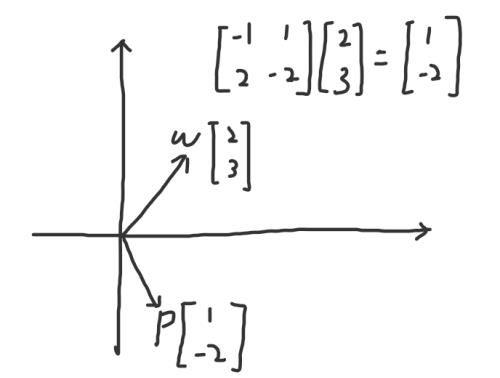
我们已经知道，矩阵和向量的乘法就相当于对该向量做了一个线性变换。在这个变换中，大部分的向量都发生了偏移，脱离了原“轨道”。举个例子：

如上图所示，向量w（2,3）在矩阵[-1,1;2,-2]的作用下，线性变换为另一个向量p（1，-2）。p和w明显不在一条直线上，发生了偏移。那有没有一个矩阵，恰好使线性变换之后新向量p和原来的向量w在同一条直线上呢？我们再看一个例子：

如上图，还是向量w（2,3），此时线性变换的矩阵变成了[1/2,1;0,2]，产生的新向量p（4,6）跟w还在同一条直线上。我们用公式可以表示成：

也就是说，矩阵A对向量v所做的线性变换，就相当于对向量v做了拉伸或者压缩，λ就是拉伸或者缩放的倍数。此时，我们将λ称作特征值，而向量v称作特征向量。

再仔细观察（1）式，是否可以把等式两边的v消去，得到A=λ呢？首先，涉及到向量的乘法是不可以直接消元的；其次，A是一个矩阵，λ是一个标量，这俩是不可能相等的。那又该怎么办呢？

这时，单位矩阵I就派上用场了。我们已经知道：Iv=vI=v，可以在（1）式的右边乘以I，得到：

此时λI就是一个矩阵了，我们把等式右边的项移到左边，再提取出公共的v，可以得到：

注意，等式右边的0是一个向量，而不是标量。（2）式说明，矩阵乘以向量，结果是0向量。这就表明，向量v经过一个线性变换后，被压缩成了一个点。我们知道，矩阵的行列式表示线性变换后面积的变化。而这里的向量v被压缩成了点，所以其对应的矩阵的行列式为0.也就是说：

给定了（3）式，我们就能求解出特征值λ，进而得到特征向量v。举个例子，我们有矩阵：

如何求它的特征值呢？首先，我们要求A-λI，可得：

然后求det（A-λI），即该矩阵的行列式：

令（4）式为0，解得λ为：

之后，我们把λ代入（2）式，就能求出向量v了（这里省略求解过程，用高斯消元法即可求得）。

说了这么多，那任何一个矩阵都有特征值和特征向量吗？我们还是来看一个例子，有一个矩阵如下：

我们可以求得det（A-λI）为λ²+4，令其等于0，得到λ²=-4。在实数范围内，不存在λ的解，因此我们说该矩阵是没有特征值和特征向量的。

线性代数的相关内容就告一段落了，下篇我们将会进行微积分的介绍，敬请期待。

本文内容由小娴整理编辑！