代数值问题的常用解法(代数值问题的例题及答案)

导语：代数最值问题的几何求解方法“三例说”

代数与几何是初中数学中的两大主角，“你中有我、我中有你”，如何使两者完美结合，找到求解问题的简捷方法。今举三例代数最值问题，一起来说说其相对应的几何求解方法：

【例1】若：x>0，y>0，且：x²＋y²=1/2，求：（√2＋1）x＋y的最大值

【分析】（图1）

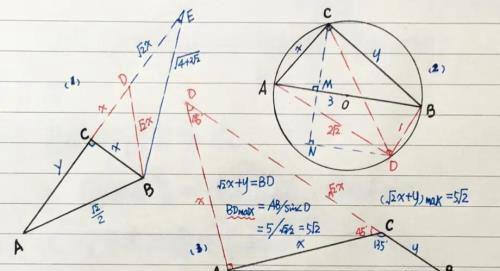
（1）作Rt△ABC，使∠ACB=90º，AC=y，BC=x，则：AB=√2/2

（2）延长AC至D，使CD=BC=x，则：BD=√2x，再延长AD至E，使DE=BD=√2x，则：AE=y＋x＋√2x=（√2＋1）x＋y

（3）△ABE为“定角对应边”，AE的最大值为△ABE外接圆直径：AB/sin∠E

（4）sin∠E=BC/BE=1/√（4＋2√2）

（5）所以：AE=（√2＋1）x＋y的最大值为：√（2＋√2）。

【例2】若：x>0，y>0，且：x²＋y²=9，求：（x＋2√2y－xy）的最小值

【分析】（图2）

（1）作Rt△ABC，使∠ACB=90º，AC=x，BC=y，则：BC=3，作Rt△ABC的外接圆O

（2）在弧AB上取点D，使BD=1，则AD=2√2

（3）由托勒密定理得：x＋2√2y=AB×CD

（4）过点C作AB的垂线垂足为M，过点D作AB的平行线交CM的延长线于点N，则：CN⊥DN

（5）由上得：CD≥CN，∴AB×CD≥AB×CN，四边形ADBC的面积=AB×CN/2=xy/2＋√2，∴AB×CN=xy＋2√2，则：AB×CD≥xy＋2√2

（6）由：x＋2√2y=AB×CD≥xy＋2√2，可得：x＋2√2y－xy≥2√2

（7）所以（x＋2√2y－xy）最小值为：2√2

【例3】若：x>0，y>0，x²＋√2xy＋y²=25，求：（√2x＋y）的最大值

【分析】（图3）

（1）由己知可得：x²＋2xy（√2/2）＋y²=5²，

（2）作△ABC，使：∠ACB=135º，AC=x，BC=y，由余弦定理可得：AB=5

（3）过点A作AC的垂线交BC的延长线于点D，则：∠D=45º，CD=√2x，BD=y＋√2x

（4）△ABD为“定角对定边”，BD的最大值为△ABD的外接圆直径：AB/sin∠D=5/sin45º

（5）所以：（√2x＋y）的最大值为：5√2

以上三例之分析，“道听度说”供参考。

本文内容由小玥整理编辑！