二元一次方程组正整数解怎么解(二元一次方程的正整数解法)

导语：正方分割，一个看似很难的问题，其实用二元一次方程组就可解

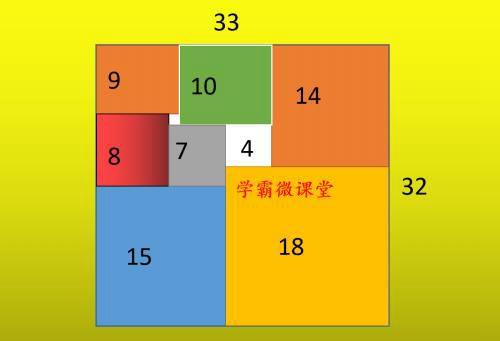
1936年，英国剑桥大学三一学院的四名学生塔特、斯通、布鲁斯和史密斯，同时对以下的正方分割产生的兴趣。正方分割是指：把正方形或者矩形分割成边长不等的小正方形。当时人们已经知道，长33宽32的矩形能够制作下图的下方分割。

尽管四名学生研究的课题是一到的，但他们考虑的侧重点各不相同。斯通从一开始就想证明：不可能对正方形进行正方分割。然而他没能证明这一点，却在探索中找到了另一个可以正方分割的矩形。

塔特等人则致力于研究正方形正方分割的理论，但他们都没能找到可以正方分割的正方形。经过几年的摸索和失败，他们开始倾向于斯通的看法，即正方分割的正方形是不存在的。

但出乎意料的是：1939年，柏林的施帕拉格居然实实在在找到了一个能够正方分割的正方形。他们很快改变了自已的研究策略，在理论的指导下，终于也找到了一个由39块正方分割的正方形。他们的研究成果被的成功的运用到电子、化学、建筑学、运筹学、通讯科学和计算机等多个学科领域，成为造福人类的有力工具。

那么四名大学生当年是怎样着手研究正方分割的呢？说起来也简单：称作一个矩形的正方分割草图，然后用尽可能少的未知数，标出每个正方形的边长，再写出这些边长应该满足的关系式，然后解这个方程组。

例如：先初画一个矩形草图，标出图中十万相邻的三个正方形边长x,y,z，然后按照以下顺序标出其余小正方形的边长x-y,2x+y,y-z,y-2z,y-3z,2y-5z,然后得到以下等量关系。

令z=1，就可以得到上述33X32的矩形正方分割。

当然按照此方法，同学们还可以不断推导出不出的正方分割。其实在数学中，有很多非常浅显的数学知识，却可以有巨大能量，可以解决很多看似不能解决的问题。通过这些问题的解决，还能激发同学们学习的兴趣，对孩子的学习有巨大的帮助。

其实关于数学兴趣的书，对家长而言是比较难挑选的，要么太高深，根本看不下去。要么太简单，孩子没有兴趣。学霸数学小编长期致力于孩子在数学方面的学习，发现《给孩子的数学三书》非常好，贴近生活实际问题，可以非常好的激发孩子的学习兴趣。

本文内容由小里整理编辑！