十字架正方形折纸教程(由正方形形拼成十字架的面积)
导语:初中数学:《正方形的性质》之“十字架”模型,课本没有哦
正方形是初中数学中一类重要的四边形,具备平行四边形的一切性质。因为正方形既是轴对称图形,又是中心对称图形,是个“完美”图形,因此它性质极其丰富,也是每年中考数学命题的热点。
本文介绍初中数学课本上没有的《正方形》“十字架”模型,希望给读者朋友们带来点启发,拓宽思路。
例题:如图,正方形ABCD边长为4,DF⊥CE。
(1)求证:DF=CE.
(2)若F是AB中点,证明:BG=BC,并求sin∠GBC=____
(3)F在运动过程中,求BG的最小值=_______
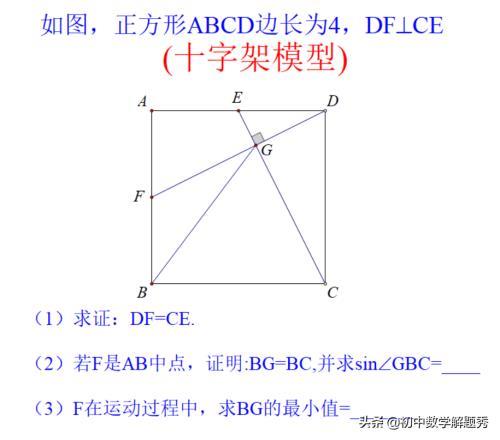
第(1)问:“十字架”模型,结论是若DF⊥CE,则DF=CE.可以用全等来证明,也可以看作是“一线三等角”模型的(平移)小推广。如图
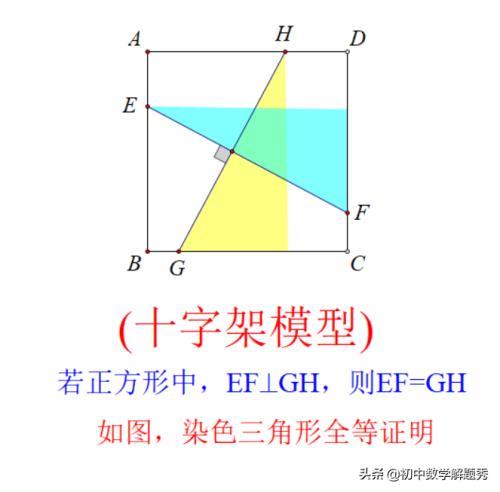
第(2)问,证明方法很多,思考角度不同,入手点不同,皆可求证计算,下面提供两种比较“精巧”的解法!
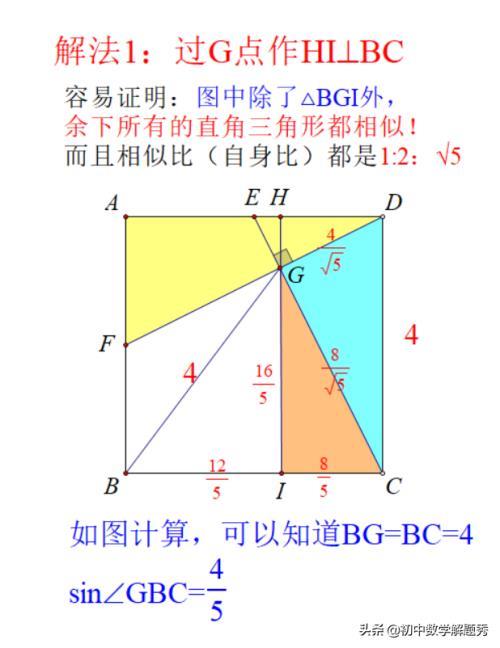
方法1:解法1:过G点作HI⊥BC,容易证明:图中除了△BGI外,余下所有的直角三角形都相似!而且相似比(自身比)都是1:2:√5。如图计算,可以知道BG=BC=4,sin∠GBC=4/5.
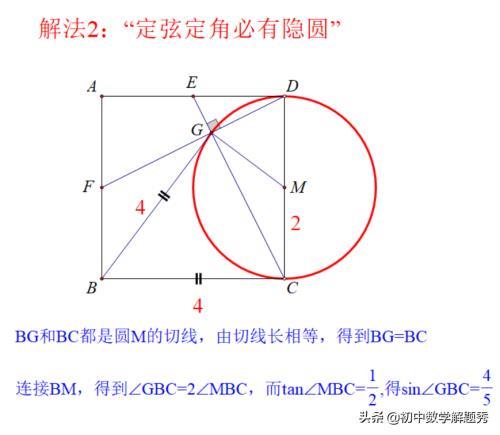
解法2:由DC=4定,DC对着的∠DGC=90°定,知道“定弦定角必有隐圆”,如图,容易证明得到:BG和BC都是圆M的切线,由切线长相等,所以BG=BC。
连接BM,得到∠GBC=2∠MBC,而tan∠MBC=1/2,得sin∠GBC=4/5。
(如何根据tan∠MBC=1/2,来求出sin∠GBC=4/5,这里面计算方法很多,不作展开。在此留给读者朋友三种计算思路;①可以是三角函数计算,②可以是半倍角构图计算,③可以是常用三角比结论,以后我会专门写一篇文章,5种方法展示计算思路。)
第(3)问:由第二问的解法2,不难看出G点的“轨迹”是以DC为直径的半圆,连接BM与圆M相交,当G是BM与圆M的交点时候,此时BG最小,可以口算:BG=BM-r=2√5-2.
写到这里,本题算是解完了,但是“余音绕梁”“不绝于耳”,还有很多种方法,甚至可以将B点作为原点构造坐标系,将正方形ABCD放在坐标系里,解析处理。而具体的计算方法,要熟练用相似三角形,三角函数,1:2:√5的放缩计算技巧,达到好思路+快计算的解题效果。
数学创作不易,欢迎大家留言评论,给出其他解法,探讨学习。欢迎大家收藏转发分享,一起前进。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请与我联系,一经查实立刻删除内容。本文内容由快快网络小楠创作整理编辑!