圆锥曲线中三角形面积求法(圆锥曲线三角形面积公式总结)
导语:高中数学:在圆锥曲线中,一个求三角形面积的简便公式
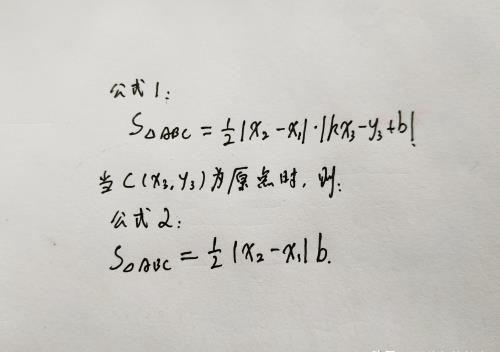
对于求三角形面积的求法,最常用的是:三角形面积=底×高÷2,或者是海伦公式,如下图所示:
而在高中的圆锥曲线中,经常会学到一条直线截圆锥曲线两点,这两点和第三点构成三角形,要求其面积或者是知道其面积求其他的量。
在此类问题中,用常规的面积公式或者海伦公式就不是那么方便了。
就此,本篇分享一个求三角形面积的简便公式,已知A(X1,Y1),B(X2,Y2)为直线L:y=kx+b上两个不同点,C(X3,Y3)为直线L外一点,则有△ABC的面积,如下图所示:
这个公式的证明可以从两点间距离和三角形面积常规面积证得,其过程如下图所示:
现在我们以两个例题,来应用这个三角形面积公式。
例1、如下图所示:
根据上面的公式,我们首先要求出直线AB的方程,将其代入椭圆方程中,根据公式1,即可求得面积,具体步骤如下图所示:
对于此题,我们也可以进行一个变式练习,将条件的倾斜角和结论三角形面积互换,即已知所围成的三角形面积,求直线方程倾斜角读书,有兴趣的读者可以尝试着做一做。
再来看看例2,如下图所示:
此题是求截距的一个问题,通用的方法是:设直线方程,代入椭圆中,利用韦达定理,根据三角形面积公式求出来。这个过程做起来相当复杂,而且又容易出错,而如果运用上述的公式2,就能够大大的简化运算过程,求出答案,其过程如下图所示:
通过上面的内容,在高中学习数学,我们是否有认真反思过自己的整个学习过程呢?
每当数学老师在课堂上给我们讲解一个方法,我们更多的是听懂了,不停地做大量习题,来巩固这样的方法。
而从来没有想过,是否可以对这些解题方法和思路,自我内化,自我吸收理解,得出自己的简便解题方法和思路,以达到事半功倍的效果。
当然,我们要注意:这样的简便不是毫无依据,是要通过严谨的数学证明得出来的。
最后,以上都是本人对圆锥曲线中,一个求三角形面积的简便公式的一些浅陋之见,耐本人能力眼界有限,有不当之处,还望读者不吝赐教。
本文内容由快快网络小楠整理编辑!