通过旋转求阴影面积的题(小学图形旋转题目的解题思路)

导语：小学数学思维拓展 图形旋转求阴影部分面积 方法巧妙 1分钟出答案

图形旋转是在小学几何题里面比较有难度的题目了，如果要想掌握这种题目的解题方法，需要多积累，本节介绍下图形旋转的基本思想：

图形旋转：就是指在平面内，把一个图形绕一个点O旋转一个角度的图形变换叫做旋转。点O叫做旋转中心，旋转的角叫做旋转角，如果图形上的点A经过旋转变为点Aˊ，那么这两个点叫做这个旋转的对应点。

旋转的几个性质：①对应点到旋转中心的距离相等。②对应点与旋转中心所连线段的夹角等于旋转角。③旋转前、后的图形全等。

旋转三要素：①旋转中心；②旋转方向；③旋转角度。

旋转要注意：三要素中只要任意改变一个，图形就会不一样。

旋转变换是解答图形问题的重要方法之一，巧妙的运用旋转，可以使复杂不规则的图形变得简单而美观。今天我们就一起来体验旋转变换给我们带来的思考。

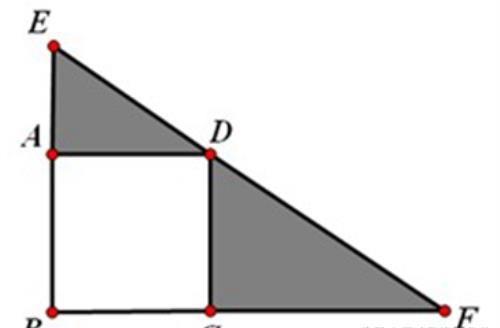
例题：正方形ABCD的边AB、BC分别在三角形BEF的BE、BF边上，顶点D在EF边上，点D把EF分成两段，DE＝12米，DF＝15米，求两个阴影三角形的面积和。

例题附图

分析：此题如果直接计算，还不太好处理，对于三角形来讲，要想计算面积，需要知道底和高，而题目里面，好像信息并不完整，中间的正方形的边长并没有告诉；

如果将三角形ADE绕D逆时针旋转90°，变成如图三角形，则可以计算出阴影部分的面积为12×15÷2＝90平方米。

本文内容由小芦整理编辑！