初中数学解直角三角形技巧大全(初中解直角三角形的方法和技巧)

导语：（二十八）初中数学之 解直角三角形 篇

一、锐角三角函数

1、定义：

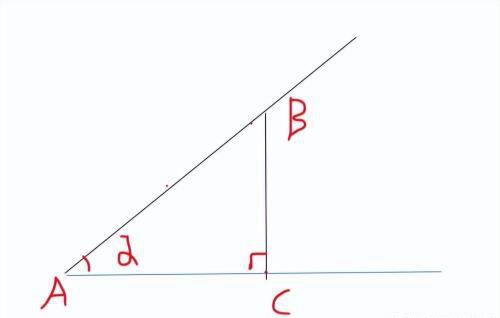
一般地，对于每一个不确定的锐角α（0°＜α＜90°），在角的一边上任取一点B，作BC⊥AC于C点，所构成一个直角三角形。而当锐角α的度数变化时，BC/AB、AC/AB、BC/AC的比值也会发生变化，因此，我们把比值BC/AB、AC/AB、BC/AC看做是关于锐角α的函数。①比值BC/AB叫做∠α的正弦，记作sinα；②比值AC/AB叫做∠α的余弦，记作cosα；③比值BC/AC叫做∠α的正切，记作tanα。④锐角α的正弦、余弦、正切统称为∠α的三角函数。

2、公式：

一般地，如果∠A是Rt△ABC的一个锐角，则有：

①sinA=∠A的对边/∠A的斜边（0＜sinA＜1）

②cosA=∠A的邻边/∠A的斜边（0＜cosA＜1）

③tanA=∠A的对边/∠A的邻边（tanA≠0）

二、解直角三角形

1、定义：

在生产实践和日常生活中，人们经常遇到一些有关三角形的边长余角度的计算。在直角三角形中，由已知的一些边、角，求出另一些边、角的过程，叫做解直角三角形。

2、例题：

已知△ABC中，AB=5cm,AC=4cm，AB与AC的夹角为α，设△ABC的面积为S（㎝²）。

（1）若α为锐角，求S关于α的函数表达式，若α为钝角时呢？

（2）何时△ABC的面积最大，并求最大面积。

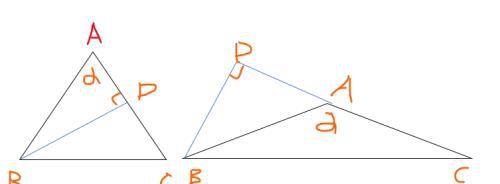
解：（1）①若α为锐角，作BD⊥AC。

在Rt△ABD中，BD⊥AD，AB=5cm,∠A=∠α

所以sinα=BD/5，BD=5sinα

所以S=1/2×4×5sinα=10sinα㎝²。（α为锐角）

②若α为钝角，延长CA，作BD⊥CD。

在Rt△ABD中，AD⊥BD，AB=5cm,∠A=∠α

所以sin（180°-α）=BD/5，BD=5sin（180°-α）

所以S=1/2×4×5sin（180°-α）=10sin（180°-α）㎝²。（α为钝角）

（2）①当α为锐角时，因为BD无最大值，即：0＜sinα＜1，所以S无最大值。

②当α为直角时，S=1/2×4×5=10cm²

③当α为钝角时，因为BD无最大值，即：0＜sin（180°-α）＜1，所以S无最大值。

综上：当α为直角时，S（最大）=1/2×4×5=10cm²

（根据此题我们可以得出一个结论：sin90°=1）

利用三角形的特性制造的工具

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小苹创作整理编辑！