矩形折叠值问题(矩形折叠值问题解题技巧)
导语:矩形-折叠:最值
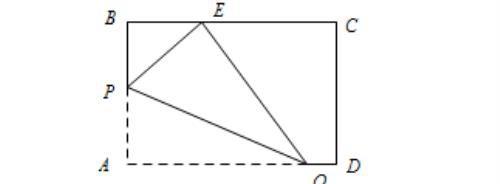
例 如图,在矩形纸片ABCD中,AB=3,AD=5,折叠纸片使点A落在边BC上的E处,折痕为PQ.当点E在边BC上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在边AB、AD上移动,则点E在边BC上可移动的最大距离为__________.
解析
(1) 由折叠,得:AP=EP,QE=QA.
∵BE≤PE,∴BE≤AP.
如下图,当P点与B点重合时, BE=PE=AB=3,即P与B重合时,BE的值最大为3.
(2) 若BE最小,则CE最大.
如下左图,CE=.要CE大,则DE必须大.DE≥QE,而QE=AQ,AQ的最大值=AD=5,
∴DE(=QE)的最大值是5,∴CE的最大值为=4,则BE的最小值为5-4=1,即Q与D重合时(如下右图),BE的值最小为1.
(3) 点E在边BC上可移动的最大距离=BE的最大值-BE的最小值=3-1=2.
答案 2
练习
1 如图,在矩形纸片ABCD中,折叠纸片使点A落在边BC上的E处,折痕为PQ.当点E在边BC上移动时,折痕的端点P、Q也随之移动.限定点P、Q分别在边AB、AD上移动.
(1) 若AB=4,AD=7,则点E在边BC上可移动的最大距离为________.
(2) 若AB=5,AD=9,则点E在边BC上可移动的最大距离为________.
解析
(1) 如下图,同例题得:当P点与B点重合时, BE值最大=AB=4.
如下图,Q与D重合时,BE的值最小.
∵CE最大值=,
∴BE的最小值=7-.
∴点E在边BC上可移动的最大距离=BE的最大值-BE的最小值
=4-(7-)=-3.
(2) 如下图,当P点与B点重合时, BE值最大=AB=5.
如下图,Q与D重合时,BE的值最小.
∵CE最大值=,
∴BE的最小值=9-.
∴点E在边BC上可移动的最大距离=5-(9-)=-4.
2 如图,在矩形纸片ABCD中,AB=6,AD=10,折叠纸片使B点落在边AD上的点E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.若限定P、Q分别在边BA、BC上移动,四边形PBFE的面积有最值吗?若有,请写出;若没有,填“无”.最大值为________;最小值为________.
1
答案 (1)-3;(2)-4
2
解析
(1) 如下图,由折叠得PB=PE,∠1=∠2.由EF∥AB得∠1=∠3,∴∠2=∠3,PE=FE,∴PB=FE,∴四边形PBFE是平行四边形.
(2) PB越大,则PE越大,PA越小,∴AE越大.
∵平行四边形面积=PB×AE,
∴AE最大,平行四边形面积最大;AE最小,平行四边形面积最小.
(3) 如下图,当P点与A点重合时,AE值最大=AB=6,
平行四边形最大面积=PB×AE=6×6=36.
(4) 如下图,Q与C重合时,AE的值最小.
∵CE=10,CD=6,∴DE=8,∴AE=2.
设PB=x,则AP=6-x,PE=x,由勾股定理得:
=+,∴x=,∴平行四边形最小面积=PB×AE=×2=.
答案 36,
本文内容由小馨整理编辑!