瓜豆原理轨迹之线段篇(瓜豆原理怎么构造)

导语：瓜豆原理、利用中位线：线段最值问题

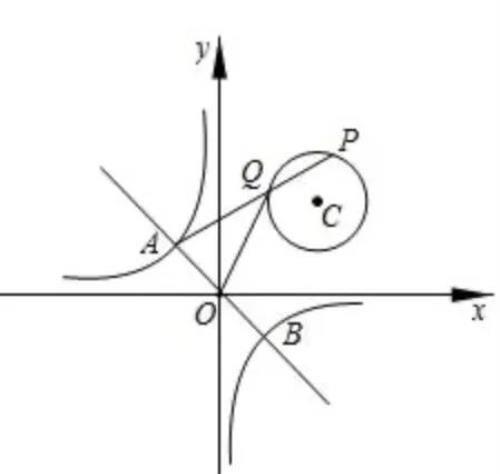
例：平面直角坐标系中，直线y=−x，与双曲线y=k/x，交与A，B两点，P是以C(2，2)为圆心，半径长为1的圆上一动点，连接AP，Q为AP中点，若线段OQ长度最大值等于2，求k的值。

方法一：瓜豆原理

分析：主动点：P，从动点：Q，中心点：A

连接AC，取AC中点D，连接CP，DQ

易证：△ADQ～△ACP

∴DQ/CP=AQ/AP=1/2

∴DQ=1/2

∴点Q运动轨迹：以D圆心，DQ为半径的⊙D上运动(定点定长)。

当：Q、D、O共线时，OQ取得最大值2

此时：OD=OQ−DQ=3/2

设：A(a，−a)，又C(2，2)

∴D［(2+a)/2，(2−a)/2］

∴((2+a)/2)²+((2−a)/2)²=(3/2)²

∴a²=1/2

∴k=−a²=−1/2。

方法二：构造中位线，OQ=1/2BP

连接PB，OQ

∵A，B关系点O对称

∴点O为AB中点

∴OQ=1/2BP

当B、C、P共线时，BP取得最大值

OQ最大值=2，BP最大值=4

∴BC=BP−CP=3

设：B(m，−m)，又C(2，2)

∴(m−2)²+(−m−2)²=3²

∴m²=1/2

例：k=−m²=−1/2。

本文内容由小竹整理编辑！