利用隐圆巧解几何题(隐圆问题怎么解决)

导语：巧用隐圆求解几何中的计算问题“多例说”

在平面几何中，有林林总总的几何计算问题，有的极有难度，有的颇具技巧。但是，我们发现有一些问题可以利用题中的隐圆来进行求解。现举几例大家一起来说说：

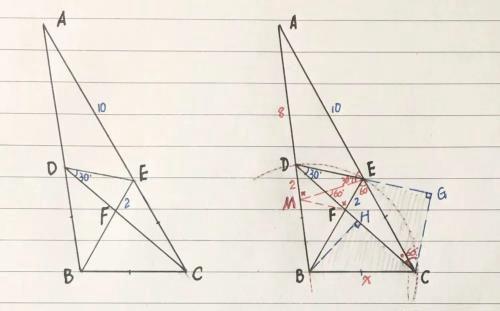
【例一】（如图）在△ABC中，点D、E分别是AB、AC边上的点，且满足：DB=BC=CE，∠CDE=30º，若：EF=2，AE=10，求AC的长

【解析】（点B为△CDE的外心）

（1）过点C作DE的垂线，垂足为G（在延长线上），则CG=CD/2，过B作BH⊥CD垂足为H，∴CH=CD/2=CG，易证Rt△CEG≌Rt△BCH，得∠BCH=∠ECG，∴∠BCE=∠DCG=60º，∴△BCE为正三角形，∴BC=BE=BD=EC，所以：点B为△CDE的外心

（2）过F作FM∥DE交AB边于点M，由BD=BE，∴∠MDE=∠FED，∴四边形MFED为等腰梯形，∴MD=2，∠DME=∠EFD=60º＋∠DCE=∠MEA，∴AE=AM=10

（3）AD=10－2=8，设BC=x，由割线定理：AE.（AE＋x）=AD.（AD＋2x），解得：x=6，所以：AC=10＋6=16

【例二】（如图）在△ABC中，∠ACB=90º，点E为AB边的中点，点L在AC的延长线上，连LE交BC于点D，过点E作AB垂线交∠LCB的平分线于点F，若：∠CAB=3∠L，EF=3，求DL的长度

【解析】（点A、C、F在⊙E上，半径为EA）

（1）由已知可得：以点E为圆心EA为半径作圆⊙E交EF于点F’，交LE于点M，连CF’，由题意可得∠F’CA=135º，而∠FCA=90º＋45º=135º，∴点F与F’重合，点F在⊙E上，EF=EA=3（半径）

（2）连接AM，设∠L=α，∠MAC=β，则：∠MAE=∠AME=α＋β，而：β＋（α＋β）=3α，所以：α=β

（3）连CE，∴圆心角∠CEM=2∠CAM=2β=2α

（4）在Rt△LCD中取斜边中点N，连CN，则：2CN=LD，且∠CND=2α=∠CEN，∴CN=CE=3

（5）所以：LD=2CN=6

【例三】（如图）△ABC中，∠C=60º，点D、E分别在边BC、AC上，AD=AB，∠EAB=∠EBA，AB=2√3，DE=1，求线段AE的长

【解析】（作正三角形造“隐圆”）

（1）以AB为边如图作正△ABF，连DF，则：AB=AD=AF=2√3，∴点A为△BDF的外心，∴圆周角∠BDF=150º，∴∠FDC=30º

（2）由∠ACB=60º=∠AFB，∴A.B.C.F共圆，得∠BCF=120º，∠ECD=∠ECF=60º，∠CFD=30º，∴∠CDF=30º=∠CFD，∴CD=CF

（3）易证△ECD≌△ECF，∴EF=ED=1

（4）由EA=EB，易证△AEF≌△BEF（sss），∴∠EFA=∠EFB=60º/2=30º

（5）在△AEF中，由余弦定理得：AE=√7

【例四】（如图）在Rt△ACB中，∠ACB=90º，AC=8√2，BC=6√2，CD为∠ACB的平分线交AB于点D，点P在CD上，且有：∠APB=135º，求：线段CP的长

【解析】（确定△ABP外接圆圆心）

（1）易得：AB=10√2，作Rt△ABC外接圆，AB为直径

（2）延长CD交圆于点Q，连接QA、QB，则：∠AQB=90º，∵∠ACQ=∠BCQ=45º，∴AQ=BQ，∴△AQB为等腰直角三角形，QA=QB=10

（3）由QA=QB，∠APB=135º，∠AQB=90º，易证：点Q为△ABP的外心（延长BQ至R，使BQ=QR，连AR，∴∠R=45º，∴RAPB四点共圆，点Q为其圆心），∴QP=QA=QB=10

（4）托勒密得8√2×10＋6√2×10=10√2QC，∴QC=8＋6=14，∴PC=QC－QP=14－10=4，即：线段PC的长为4

以上四例之分析，“道听度说”供参考。

本文内容由快快网络小海整理编辑！