向量有关三角形的结论(向量中构成三角形的条件)

导语：向量在三角形中的几个重要结论—外心

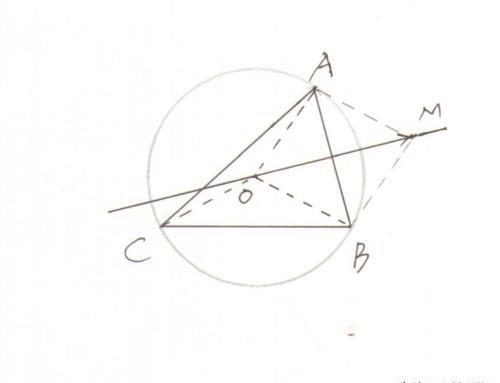
外心：三角形三条垂直平分线的交点。设O是三角形ＡＢＣ所在平面内一点，则Ｏ为三角形ＡＢＣ外心的条件是|OA|=|OB|=|OC|，即点O到三个顶点的距离相等，或（OA+OB）AB=（OB+OC）BC=（OC+OA）CA=0.（黑体字代表向量）（OA+OB=OM，OMAB，所以（OA+OB）AB=0）

知识回顾：

在三角形ABC中，直线l、m、n分别为三条边的垂直平分线，记l，m的交点为O，则根据垂直平分线性质，得到AO=BO，BO=CO，所以AO=CO，得到O也在直线n上。因此，三角形的三条垂直平分线交于一点，其交点为外心。

外心的性质：

（一）外心到三顶点的距离相等，即外心是三角形外接圆的圆心。

（二）过外心作一边的垂线平分此边。

（三）外心与一边中点的连线垂直于此边。

（四）直角三角形的外心就是斜边的中点，锐角三角形的外心在三角形内，钝角三角形的外心在三角形外。

本文内容由小迪整理编辑！