角度大小的比较方法有哪些(角的大小与什么有关)

导语：一道初中题-有关角度大小的对比

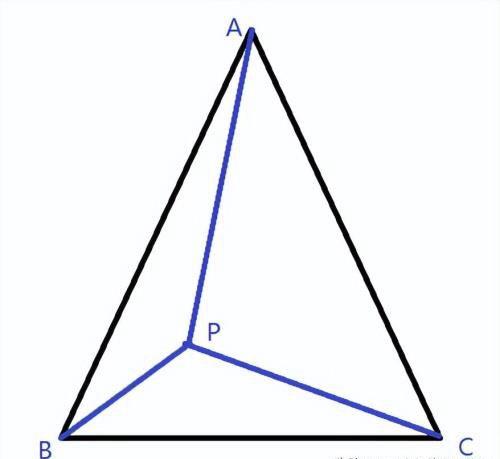
一道初中题-有关角度大小的对比

在三角形ABC中， AB=AC， P是三角形ABC内的一点， 并且有∠APB>∠APC。

证明∠BAP>∠PAC.

证明：直观地看，PC的长度明显大于PB的长度，但证明不应该这样基于直觉。因此我们需要逻辑证明它。

如下图构造一个三角形。

在三角形ABC的外侧构造一个三角形CAQ， 使得∠CAQ=BAP，并且AQ=AP， 因此三角形△BAP全等于三角形△CAQ。

这样∠AQC=∠APB>∠APC (1)

另外AP=AQ， 说明：

∠AQP=∠APQ （2）

我们用（1）-(2)可以得出：

∠AQC-∠AQP>∠APC-∠APQ

这样相减后得出的角度是△PQC的两个角，即：

∠PQC>∠QPC

这样PC>QC

而前面证明了三角形BAP全等于三角形CAQ，

QC=PB

因此：

PC>PB

下面比较三角形APB和三角形APC，

因为AB=AC

AP=AP，

但PC>PB

根据三角形的一个定理：若两个三角形的夹边相等，那么夹角的对边的长度的大小是和该夹角正相关的，即较大的边对应着较大的角，反之亦然。

由此证明出：

∠BAP>∠PAC.

本文内容由小楠整理编辑！