高矮排队方法(高个矮个游戏玩法)

导语：高矮个子排队题解-python(贪心算法)原创

题目描述先有一队小朋友，他们高矮不同，我们以正整数数组表示这一队小朋友的身高，如数组{5,3,1,2,3}。我们现在希望小朋友排队，以“高”“矮”“高”“矮”顺序排列，每一个“高”位置的小朋友要比相邻位置高或者相等；每一个“矮”位置的小朋友要比相邻的位置矮或者相等；要求小朋友们移动的距离和最小，第一个从“高”位开始排，输出最小移动距离即可。例如，在示范小队{5,3,1,2,3}中，{5,1,3,2,3}是排序结果。{5,2,3,1,3}虽然也满足“高”“矮”“高”“矮”顺序排列，但小朋友们的移动距离大，所以不是最优结果。移动距离的定义如下所示：第二位小朋友移到第三位小朋友后面，移动距离为1，若移动到第四位小朋友后面，移动距离为2；输入描述5，3，1，2，3输出描述5，1，3，2，3

题解：

该题目求解最小移动距离，属贪心算法，求局部最优解以达到全局最优。

题目要求以“高”“矮”“高”“矮”顺序排列，我们都知道任意顺序三个数我们移动一步距离就能排出“高矮高”或“矮高矮”，该题目的局部是指从列表第一个元素“高位置”开始连续三个数字进行判断。

算法实现：通过对列表的遍历和元素位置交换实现。

1、从初始“高”位置开始连续三个数值lis[i]、lis[i+1]、lis[i+2]判断，如果lis[i]数值不是最小的，就不需要移动位置，因为“高”-“矮”-“高”有两个高位置。判断当前i+2位置是不是最后位置，如果是需要判断lis[i+1]、lis[i+2]位置高矮值，然后退出循环；如果不是最后位置则i+=1，判断下一个“矮”位置。

2、对于“矮”位置存在三种情况

第一种：连续三个数中，当前lis[i]最小，则不需要移动位置。

第二种：连续三个数中，当前lis[i]最大，则需要与后面lis[i+1]交换位置。

第三种：连续三个数中，当前lis[i]大于lis[i+1]，小于lis[i+2]，则需要lis[i+1]与lis[i+2]交换位置。

因“高”位置对列表结尾位置作了判断，所以“矮”点就不存在i超出的问题。

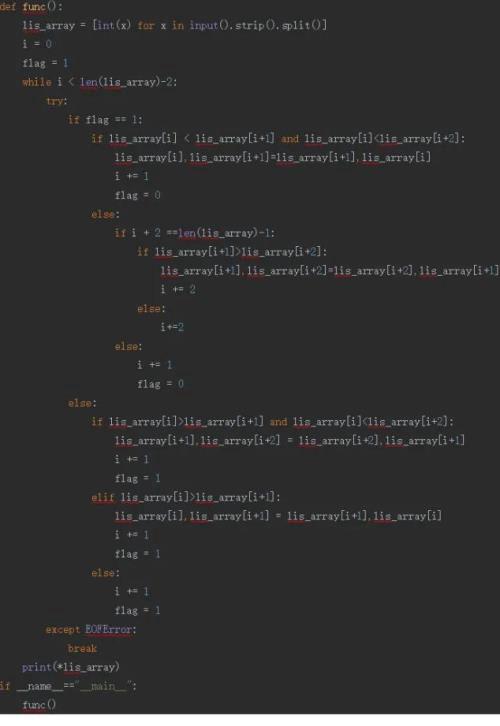
源码截图：

源码

运行结果：

如果对大家有所帮助，请点个赞，让小编也高兴高兴。

本文内容由小涵整理编辑！