凸函数证明例题(怎么证凸函数)

这是凸函数一个充要条件。它是从凸函数的定义不等式中派生出来的。凸函数的定义不等式(以“上凸函数”为例)是：f(λx1+(1-λ)x2)≥λf(x2)+(1-λ)f(x1). 这个充要条件是不等式左侧关于λ的函数与f(x)有相同的凸性. 以证明题的形式表示为：

证明：f为I上的凸函数的充要条件是对任何x1,x2∈I，

函数φ(λ)=f(λx1+(1-λ)x2)为[0,1]上的凸函数.

充分性比较好证明：

证：[充分性]若φ(λ)=f(λx1+(1-λ)x2)为[0,1]上的上凸函数, 则

对任意γ∈(0,1), 使得φ(1-γ)≥γφ(0)+(1-γ)φ(1), 【这里只对λ1=0,λ2=1应用凸函数的定义公式】

即f((1-γ)x1+γx2)≥γf(x2)+(1-γ)f(x1), 【其中φ(0)=f(x2), φ(1)=f(x1)】

由x1,x2和γ的任意性，知f为I上的上凸函数 , 充分性得证！

必要性的证明虽然看起来复杂一点，但如果不细看，你是不知道它到底有多复杂的。

[必要性]若f为I上的上凸函数 , 则对任何x1,x2∈I，

任意λ∈(0,1),任何t1,t2∈[0,1], 有λt1+(1-λ)t2∈(0,1),

φ(λt1+(1-λ)t2)=f((λt1+(1-λ)t2)x1+(1-(λt1+(1-λ)t2))x2)

=f(λ(t1x1+(1-t1)x2)+(1-λ)(t2x1+(1-t2)x2))【t1x1+(1-t1)x2，t2x1+(1-t2)x2∈I】

≥λ(t1x1+(1-t1)x2)+(1-λ)(t2x1+(1-t2)x2)=λφ(t1)+(1-λ)φ(t2),

即φ为[0,1]上的上凸函数 , 必要性得证！

综上φ(λ)在[0,1]上上凸是f为I上的上凸函数的充要条件.

同理可证φ(λ)在[0,1]上下凸是f在I上下凸的充要条件.

这里最让人摸不着脑袋的是，怎么知道要把“f((λt1+(1-λ)t2)x1+(1-(λt1+(1-λ)t2))x2)”转化成f(λ(t1x1+(1-t1)x2)+(1-λ)(t2x1+(1-t2)x2))的?

其实这是一个逆向思维的过程：

要使φ(λt1+(1-λ)t2)≥λφ(t1)+(1-λ)φ(t2),

即f((λt1+(1-λ)t2)x1+(1-(λt1+(1-λ)t2))x2)

≥λf(t1x1+(1-t1)x2)+(1-λ)f(t2x1+(1-t2)x2),

又(λt1+(1-λ)t2)x1+(1-(λt1+(1-λ)t2))x2

=λt1x1+t2x1-λt2x1+x2-λt1x2-t2x2+λt2x2，

λ(t1x1+(1-t1)x2)+(1-λ)(t2x1+(1-t2)x2)

=λt1x1+λx2-λt1x2+ t2x1-λt2x1+x2-t2x2-λx2+λt2x2

=λt1x1-λt1x2+ t2x1-λt2x1+x2-t2x2+λt2x2，

∴f((λt1+(1-λ)t2)x1+(1-(λt1+(1-λ)t2))x2)

=f(λ(t1x1+(1-t1)x2)+(1-λ)(t2x1+(1-t2)x2)).

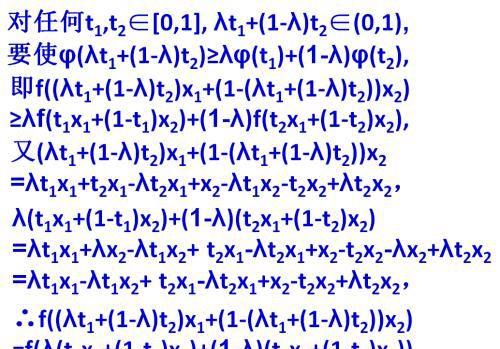
题外的这一段推导，其实才是这道题最困难的地方！很多高数问题，都把最困难的一步隐藏起来，这也是一些人老是学不好高数的重要原因之一。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小悦创作整理编辑！