七年级环形跑道问题公式(初中数学环形跑道问题)

导语：初一数学难点：路程问题之环形跑道及船只航行问题解密

在之前，讲过的路程问题中，主要是对类型一一般的行程问题，即直线上的追及相遇问题，做了一些概念介绍以及思路总结。今天我们主要探究的就是路程问题中的其他两个类型：环形跑道与时钟问题以及船航行与飞机飞行问题。

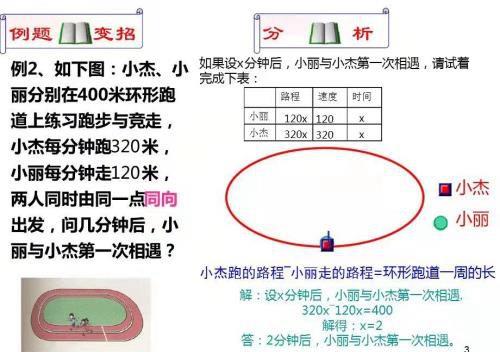
一、环形跑道与时钟问题。首先说明一下环形跑道追及相遇问题。在环形跑道上运动时，甲乙要相遇，需要背向而行，在甲乙两人相遇时，两人所行驶的路程之和即为环形跑道的长度，所以背向而行时，涉及到的公式为：甲行驶路程＋乙行驶路程＝环形跑道长度；甲乙两人要追及，则以同时同地同方向这种情况分析，一开始甲乙都在起点，那么在开始运动以后，速度快的甲肯定在速度慢的乙前面，那么乙是不可能追上甲的，只能甲追乙，那么此时环形跑道就可以表示成直线追及问题即甲在起点，乙在距离甲一个环形跑道长度的前方，然后利用直线追及问题解决，涉及到的公式为：甲行驶路程－乙行驶路程＝环形跑道长度。

接下来说明一下时钟问题，时钟问题主要是时针与分针的追及与相遇问题，我们只要理清时针与分针的运动的起点及速度，便可解决问题，通常情况下，我们一般是把时钟问题看做是整时整分为起点的同向追及问题来分析。在钟面上，我们知道，一共有12个大格，周角是360 度，则一个大格是30度，而时针走一个大格是1小时，故时针走1分钟是0.5度，分针转一周是60分钟，则分针走1分钟是6度。掌握了时针与分针的运动速度，我们在做题时就可以从12点作为起点，去寻找时针与分针转过的角度上的等量关系了。有些这些思路，在做同类型题时，最起码不会两眼一抹黑，不知所措了。

二、船航行与飞机飞行问题。此类问题主要涉及到外力条件对运动速度的影响。在你顺风或者顺流行驶时，风或水是给你加速的，在你逆风或者逆流行驶时，风或水是给你减速的，故清楚了这些概念以后，我们把可能要用到的公式给简单整理一下：

1.顺水（顺风）速度＝静水（静风）速度＋水流（风）速度

2.逆水（逆风）速度＝静水（静风）速度－水流（风）速度

3.水流速度＝（顺水（风）速度－逆水速度）÷2

当理解并掌握了这些公式，在做这类型题时，把题意分析清楚以后，就可以直接找到等量关系，列出方程。解决问题。

无论这些应用题的题目都多长，题意有多复杂，只要抓住题中条件，找到对应的等量关系及公式，那么解决问题就不再是难事。

关注张老师，让你的孩子成绩更好！亲子关系更和谐！

本文内容由小姬整理编辑！