维空间的特征(维空间有多少个基)

导语：n维空间的基本类型探讨

目前所能够知道的维度空间类型有，零维空间，一维空间，二维空间，三维空间，目前猜测存在着四维空间的可能性。本文对维度空间的类型研究，正是希望通过对一个n维空间的特性及不同n维空间的联系，找到四维空间的可能具备的属性。然后利用这些属性为线索，在自然界中寻找出对应的证据及推理来论证四维空间的存在性。

一个n维空间的一个独立的物体的几何需要至少n个参数来描述。n是指大于等于0的整数。反过来讲，一个n维物体无法使用（m<n,m为非负整数）m个参数来进行描述。

这个概念的物理意义有两个，第一个是n维物体无法在m维空间中，以n个参数构成的物体存在。需要将n维物体以逐一递减的进行降维处理。第二是n维物体在k(n<k)维空间，只能以k维物体的组成成分存在，需要进行升维处理。

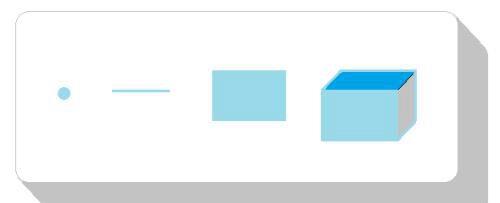
零维空间是n维空间的单元空间，它是构成高维空间的基础。 在数学几何中用点来表示，而在自然世界中的物理意义是一个虚无的事物，关于虚无的讲述超过本文的主题，会在后面文章再发表给读者阅读。其次，零维空间没有矢量的概念。

一维空间的数学几何表示是一条线。一条线至少由两个接触的点及接触处所构成。一维空间有矢量的概念，即它在某一时刻只能往两个不重合方向扩展。推导出，一个一维空间由无数个零维空间构成。物理意义上来讲，一个个零维空间是如何构成一维空间的，不在本文的讨论范围，将会后面文章进行表述。感兴趣的读者可以点击右上角“关注”，及时获取后续的文章发表。

二维空间的数学几何表示是一个面。一个面至少由两条互交的线及它们的交点构成。二维空间有矢量的概念，即它在某一时刻只能往两对互相垂直且每对的方向相反的方向扩展。一个面除了可以用线构成，也可以用点来构成面。一个二维空间可以看作由无数个（有限小的一维空间）一维物体构成。却不能直接说是一维空间们直接构成二维空间。在物理世界可以解释这个原因。原因如下：

n维空间具有容纳独立的n维物体的特性，对于它所处的维度下，不存在容量的边界概念。但有最少值的概念，这个由某个时刻下，所容纳的物体量决定。所以选择在某一维空间中直接的方式会迷乱在空间的无限大特性中。

三维空间的数学几何表示是一个立体。一个立体至少由两个相交的面及它们的线构成。三维空间有矢量概念，即它在某一时刻只能往在三对互相垂直且每对的方向相反的方向扩展。一个立体除了可以用无数个面构成，也可以用无数条线构成，更可以用无数个点来构成。

根据对各个n维空间的特性挖掘及不同n维空间的联系。总结如下这样的规律：

（0<n≤3，n∈N）、（0≤m<n）

1. 两个n维空间的相交是一个（n-1）维空间。

2. n维空间的边界是至少一个m维来体现。

3. （n-1）维空间的边界上插入一维空间，一与（n-1）个参数的方向互相垂直。且（n-1）维没有原先具有的方向。

4. n维空间在某个时刻存在着具体的至少容量。（没有最大的容量限制，暂时假定）

根据上述内容，四维空间可能具备的特性是，两个四维空间相交处是一个三维空间，四个参数的方向互相垂直情况且 一个参数的两个方向是相反方向进行四维空间的扩展，欢迎读者进行补充。​

阅读了本文的读者，是否对维度空间的类型有所了解呢，或者本文的内容令你产生某种看法、想法呢！欢迎发表您的真知灼见，为维度空间的研究提供新思路。

本文内容由小姿整理编辑！