数据结构AVL树(avl树构造)
导语:数据结构 --- AVL树
数据结构 --- AVL树
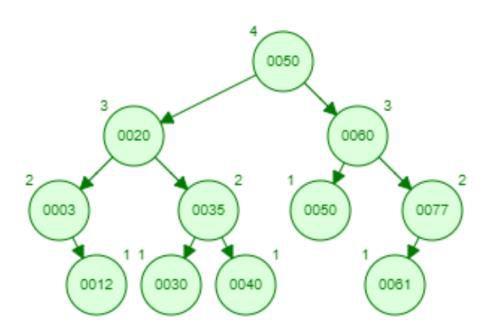
AVL(Adelson-Velsky and Landis Tree) 树是一种自平衡二叉树, 也是最早发明的一种自动平衡二叉树。原因是由于BST(二叉搜索树)在用有序列表不断插入时会退化成链表而大大影响其效率,因此最早计算机科学家G. M. Adelson-Velsky和Evgenii Landis在1962年发明了AVL树。首先要明确AVL树是一种二叉搜索树(BST),不了解BST的同学可以看我之前的一篇文章<<数据结构---二叉搜索树>>。AVL树中的任意节点的两颗子树高度差<=1。因此AVL树是高度平衡的。如下图所示的就是一颗AVL树。每个节点都标注了其高度。
在AVL树中把每个节点的左子树高度减去其右子树高度差定义为平衡因子。在AVL树中只有平衡因子大于等于-1并且小于等于1才是平衡的。因此平衡因子只能取3个值-1, 0和1。平衡因子取其它值被认为是不平衡的,就需要对该AVL树进行调整,以使其达到平衡。
当一颗AVL树不平衡时,我们需要对其进行一系列操作使其保持平衡,下面介绍AVL树的基本操作。
左旋上图是节点的原始状态,绕y节点进行左旋的步骤如下:
如果β不为空将β的parent设为x,同时将x的右孩子设为β。如果p是NULL,将y设为根节点。否则如果x是p的左孩子,将y设为p的左孩子否则将y设为p的右孩子将p设为y的父节点将y设为x的父节点,将x设为y的左孩子,完成左旋。右旋上图是节点的原始状态,绕x节点进行右旋的步骤如下:
如果β不为空,将β的父节点设为y,同时将y的左孩子设为β。如果p是NULL,将x设为根节点否则,如果y是p的右孩子,将p的右孩子设为x否则,将p的左孩子设为x将x的父节点设为p将x设为y的父节点,将y设为x的右孩子,完成右旋左右旋转(LR)如下图,左右旋转是将x以y为中心左旋。
然后再以y为中心对z进行右旋,完成平衡调整。
右左旋转(RL)如下图,先以y为中心对x进行右旋。
然后再以y为中心对z进行左旋,完成平衡调整。
上面我们介绍了AVL树的基本操作,下面我们介绍AVL树的插入和删除算法。
插入算法假设当前AVL树的初始状态如下图所示:
上图所示的AVL数每个节点的值和平衡因子都标了出来。它现在处于平衡状态,因为它的每个节点的平衡因子(左子树高度减去右子树高度的值)都满足要求(大于等于-1并且小于等于1)。现在假设我插入一个值为9的节点,我们来分步看看插入算法的整个过程。
首先按照BST的插入算法,插入值为9的节点。插入后,如下图所示:可以看到,上面的树不再平衡,因为树中有三个节点的平衡因子为2,所以需要对其进行调整使其满足AVL树的性质。调整如下:看下图棕色虚线框的部分,也就是插入节点后导致不平衡的部分,它满足左右旋转的特点。因此对其进行左右旋转。
左右旋转后得到下图:
从上图可以看出,该AVL树已经平衡。
删除算法从AVL树中删除一个节点,可以按照BST删除节点的方法先删除该节点,由于删除后AVL树可能不平衡,因此需要进行调整。假设要删除下面这颗AVL树的值为13的节点。删除过程如下:
按照BST的方法删除值为13的节点,删除后结果如下图所示:重新计算各个节点的平衡因子,如下图所示:值为21的节点平衡因子为2,因此需要调整。
调整该AVL数,使其平衡。以上图中棕色框值为9的节点为中心,将值为21的节点右旋,右旋后得到下图:
再对上图的各个节点重新计算平衡因子得到下图:
从上图可以看出,各个节点的平衡因子均大于等-1并且小于等于1,所以调整完成。该AVL数达到平衡状态。
对于AVL数的遍历,查找均和BST树一样,不再介绍,同学们可以参考我之前的文章<<数据结构---二叉搜索树>>。
下面是AVL树的python代码实现:
Create a tree node
class TreeNode(object):
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1
class AVLTree(object):
Find the correct location and insert the node
if not root:
return TreeNode(key)
elif key < root.key:
root.left = self.insert_node(root.left, key)
else:
root.right = self.insert_node(root.right, key)
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
Function to delete a node
def delete_node(self, root, key):
Update the balance factor of nodes
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
balanceFactor = self.getBalance(root)
Function to perform left rotation
def leftRotate(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
Get the height of the node
def getHeight(self, root):
if not root:
return 0
return root.height
34;{0} &34;& Print the tree
def printHelper(self, currPtr, indent, last):
if currPtr != None:
sys.stdout.write(indent)
if last:
sys.stdout.write(&34;)
indent += &34;
else:
sys.stdout.write(&34;)
indent += &34;
print(currPtr.key)
self.printHelper(currPtr.left, indent, False)
self.printHelper(currPtr.right, indent, True)
myTree = AVLTree()
root = None
nums = [33, 13, 52, 9, 21, 61, 8, 11]
for num in nums:
root = myTree.insert_node(root, num)
myTree.printHelper(root, &34;, True)
key = 13
root = myTree.delete_node(root, key)
print(&34;)
myTree.printHelper(root, &34;, True)
本文内容由小馨整理编辑!