> 教育
用换元法巧解初中数学题(换元法解题过程)
导语:一题多解,换元法很常用,几何法新奇。详细解析初中数学题114。
解方程:√16-x²+√9-x²=5
解:方法一:
令√16-x²=m,√9-x²=n,
则m+n=5,①
又m²=16-x²,n²=9-x²,
∴m²-n²=7
∴(m+n)(m-n)=7,②
将①代入②得m-n=7/5,③
由①和③联立方程得m=16/5,
∴√16-x²=16/5,
∴x²=16-(16/5)²=144/25
∴x=±12/5。
方法二:令√16-x²+√9-x²=5为①
再令√16-x²-√9-x²=t为②,
由①x②得,
16-x²-(9-x²)=5t,
∴7=5t,
∴t=7/5,
又由①+②得,
√16-x²=16/5,
∴x²=16-(16/5)²=144/25
∴x=±12/5。
方法三:直解。
对√16-x²+√9-x²=5两边平方得,
16-x²+9-x²+2√(16-x²)(9-x²)=25
整理得x²=√(16-x²)(9-x²),
等式两边再平方得,
x⁴=144-25x²+x⁴,
∴25x²=144,
∴x²=144/25,
∴x=±12/5。
方法四:几何法
由√16-x²+√9-x²=5可知,
√4²-x²+√3²-x²=5,
联想勾股定理,
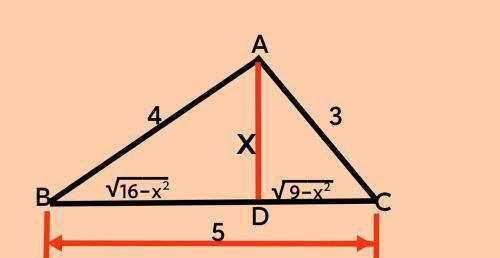
构造两个有公共直角边x的直角三角形,
如下图所示,
由图可知,x就是Rt△ABC斜边上的高,
我们用面积法去求x,
因为S△ABC=AB·AC/2
=BC·AD/2,
即4×3/2=5x/2,
解得x=12/5。
此时应注意,因为我们把情景设定在直角三角形中,
一定是x=12/5,
但因为(±x)²=x²
对于x=-12/5实际也是适应的,
故x=±12/5。
本文内容由小思整理编辑!