三角形的五心都是什么(三角形中的五心口诀)

导语：数学中三角形的“五心”你会了吗？教你马上学会。（中考生必看）

三角形五心是指三角形的重心、外心、内心、垂心、旁心。

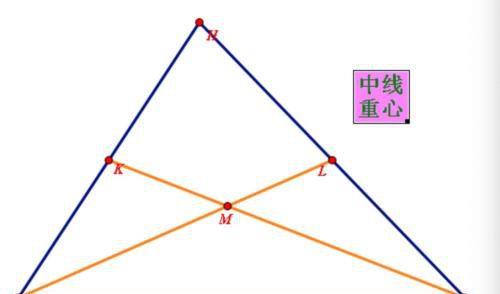
【重心】

三条中线的交点是重心。

口诀：三条中线定相交，交点位置真奇巧，交点命名为“重心”，重心性质要明了，

重心分割中线段，数段之比听分晓；长短之比二比一，灵活运用掌握好。

老师支招小技巧：重心意味着平稳，举个例子，站在公交车上，你的重心要稳，这样才不会摔倒，就像人站在一个跷跷板上，怎样不会摔倒，那肯定是站在“中间”保持平衡。所以重心是“中线”的交点！其中重心到顶点与重点到此中点的线段比为2:1，此知识考的非常多。

【垂心】

三角形三条高线的交点为垂心。

口诀：角形上作三高，三高必交于垂心，高线分割三角形，出现直角三对整，

直角三角形有十二，构成六对相似形，四点共圆图中有，细心分析可找清。

老师支招小技巧：分清锐角三角形，直角三角形，钝角三角形的高；

三角形的垂心，顾名思义，垂直垂直，所以是指三角形高线的交点。一条高线将三角形分成两个直角三角形，三条高线分成12个直角三角形，构成6对相似三角形。

【内心】

三条内角平分线的交点为内心。

口诀：三角对应三顶点，角角都有平分线，三线相交定共点，叫做“内心”有根源，

点至三边均等距，可作三角形内切圆， 此圆圆心称“内心”，如此定义理当然。

老师支招小技巧：角平分线都是在三角形内部的，故交点也在其内部，故以此记忆其内心区别。

根据角平分线的性质：角平分线上的点到线两端的距离相等，结合图形，由此可知：内心到三角形三边的距离相等。所以内心也是三角形内切圆的圆心。

【外心】

三边垂直平分线的交点是外心。

口诀：三角形有六元素，三个内角有三边，作三边的中垂线，相交共一点，此点为外心，

用它可作外接圆。内心外心莫记混，内切外接是关键。

老师支招小技巧：外心是外接圆的圆心，圆心到外接圆的长度都一样，即圆心到三角形三个顶点的距离都一样。

结合图形，以及中垂线的性质：线段中垂线上的点到线两端的距离都相等，故可知为什么中垂线的交点到三角形三个顶点的距离相等了。

【旁心】

与三角形的一边及其他两边的延长线都相切的圆叫做三角形的旁切圆，旁切圆的圆心叫做三角形旁心。

中考题当中，经常考到等腰三角形和等边三角形的三线合一，这就涉及到三角形的重心，垂心，内心，一定要学会区分，在考圆的知识当中便会经常出现内切圆，外切圆，弄清楚与三角形的关系，那就迎刃而解了！你学会了三角形的五心了吗？

本文内容由小悦整理编辑！