数学中的φ2怎么求(求丌的方法)

导语：初中数学：如何求sin15°？十种方法总有一个适合你

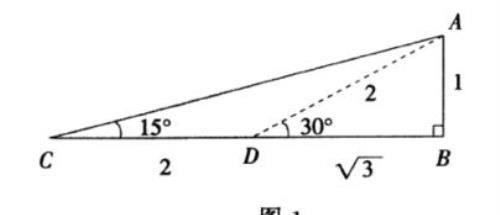
∠如图1 ,在Rt⊿ABC中，∠B=90°,∠C=15°.我们不妨将它称为解决此问题的基本图形.

在这个三角形中要求sin 15º，目前显然没办法直接得出比值AB/AC。但我们知道直角三角形中，30 º,45 º,60 º这几个特殊角的三角函数值，所以考虑基本图形与含特殊角的直角三角形的关系，就是顺理成章的.

一、考虑15 º与30 º的关系

方法一 如图1.

方法二 如图2.

方法三 如图3.

方法四 如图4.

作顶角为30º的等腰⊿ABC，其中∠A=30°过B点作AC的垂线BD，垂足为D，则∠DBC=15°.

方法五 如图5.

作顶角为30º的等腰⊿ABC，其中∠A=30°,AD为底边BC上的高.

二、考虑15º与45º的关系

方法六 如图6.

作Rt⊿ABC,∠B=90°，∠ACB=15°，延长BA到D点，使BD=BC，连接DC，则∠ACD=30°.作AE⊥DC于E.

方法七 如图7.

方法八 如图8.

作Rt⊿ABC，∠B=90°,∠ACB=30°,延长BA到D点，使BD=BC，连接DC，则∠ACB=15°，作

AE⊥DC于E.

三、考虑15º与60º的关系

方法九 如图9.

作Rt⊿ABC，∠B=90°，∠ACB=60°，在AB上取点D，使∠ACD=15°.过点D作DE⊥AC于点E，垂足为E.

以上解法是从寻找15º角与其他特殊角的关系出发，寻找“基本图形”与其他“特殊”直角三角形的联系，通过计算得出sin15º的值.“基本图形”往往是在其他图形中构造出来的，但在方法一和方法六中，则是由”基本图形“构造出了特殊图形.

四、由”基本图形“构造一个特殊图形.

方法十 如图10，构造边长为1的正方形ABCD，在BC上取点E，使∠EAB=15°，在DC上的取点F，使∠FAD=15°，连接AE,AF,EF.显然有

以上方法都是由具体角、特殊角构造图形解决问题.我们还可从15º和30º的关系，尝试一个角和它的两倍的关系，从而得到其它方法，此略.

您给我转评赞，有一样就谢谢您了！

本文内容由小珊整理编辑！