三角尺的面积怎么求(使用三角尺)

导语：巧用三角尺特性 速求图形面积（5）

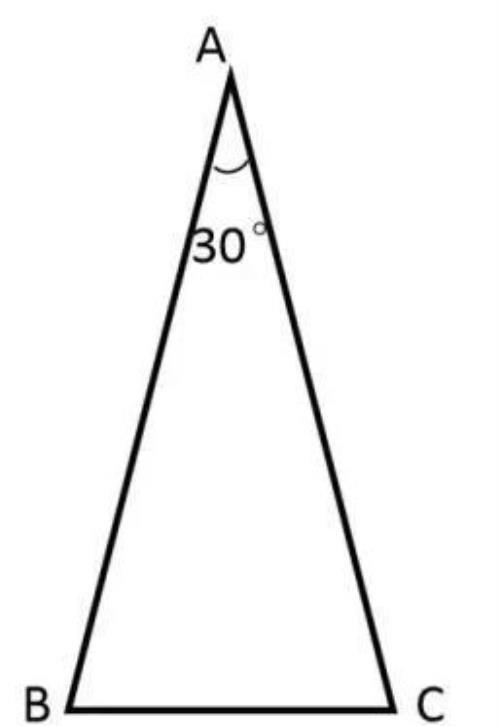
如图，

在▲ABC中，AB=AC=8cm,∠A=30°,则▲ABC的面积是多少平方厘米？

解析：过B点作BD⊥AC（如下图）

在▲ABD中在,∠ADB=90°, ∠A=30°,则BD=AB÷2= 8÷2=4(cm)

S▲ABC=AC×BD÷2=8×4=16(平方厘米)

【小贴士】此题根据已知条件和三角尺特性巧作三角形高，从而快速解决问题。

附：三角尺特性

一、含45°角的直角三角尺（等腰直角三角尺）

1. 角：∠A=∠C=45°,∠ABC=90°

2. 边：①2条直角边长度相等，即AB=CB

②斜边上的高=斜边的一半，即AC=2BD

3. 面积：①直角边的平方÷2

②斜边的平方÷4

二、含30°角的直角三角尺

1.角：∠A=60°∠B=90°,∠C=30°

2.边：30°角所对短直角边=斜边的一半，即AC=2AB

4.面积：长直角边×短直角边÷2

【举一反三】你能快速求出下图阴影部分的面积吗？聪明的你试试看

图中三角形均为等腰直角三角形，线段长度如图所示,AB=10cm,BE=8cm，EC=2cm，则阴影部分的面积是多少平方厘米？

本文内容由小林整理编辑！