求证角平分线和中线重合的三角形是等腰三角形(角平分线中线合一怎么证全等)

导语：中考几何压轴 66 比例性质运用 求证角平分线与中线结合 所属性质

中考几何压轴 66 比例性质运用 求证角平分线与中线结合 所属性质

这一系列，不限专题，解析系列经典几何题，提高几何分析解决问题能力。

题73. 《角平分线与中线相遇》

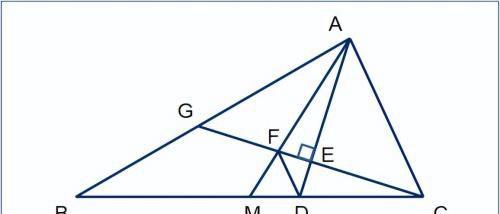
如图，△ABC中，AD是角平分线，AM是中线，CG⊥AD于E，交AM于F。连接FD，求证FD∥AC。（AB＞AC）

〖一般性提点〗

两直线平行的证明

[1]. 两直线被第三条直线所截的同位角相等；或者内错角相等；

[2]. A型相似；或者X型相似

[3]. 证明平行四边形的方法，例如：四边形对角线互相平分等。

题设似应增加一条AB≠AC，不然D、E、F、M缩并成一点。不妨设AB＞AC。

[4]. 比例的性质：比例的恒等变换

经常用比例性质，对比例线段进行变换。比例的性质缩并如图所示，其中，m、n、p、q是任意常数，且不使任何分子、分母为零。

例如：b/a＝d/c，(a+b)/b＝(c+d)/d，a/(a+b)＝c/(c+d)，a/(b-a)＝c/(d-c)等。

注意，等式a/b＝c/d称为比例。“比例a/b”是一种错误的说法。上述恒等变换中，虽然具体的比可能变化，但比例关系不变。

〖题目分析〗

欲证明DF∥AC，只需证明（△ACM中）

DM/CD＝FM/AF：

根据角平分线性质，易知E为CG中点，AG＝AC；

连接EM，是△CBG的中位线，EM∥＝BG/2；BM＝CM，☞ BD-2DM＝CD

在△ABD中，EM∥AB：

DM/BD＝EM/AB

☞ DM/(BD-2DM)＝EM/(AB-2ME)

☞ DM/CD＝EM/AG

〖注〗这个比例也可由角平分线定理得出如下：

BD/CD＝AB/AC

☞ (BD－CD)/CD＝(AB－AC)/AC

☞ 2DM/CD＝BG/AC

☞ 2DM/CD＝2EM/AC；（BG＝2EM）

☞ DM/CD＝EM/AG；（AC＝AG）

再由EM∥AG知△EFM∽△GFA：

FM/AF＝EM/AG

∴ DM/CD＝FM/AF，☞ DF∥AC。

本文内容由小娴整理编辑！