证明线段不等关系的方法(证明线段相等的典型题)

导语：初中数学：证明线段不等关系或最值问题常用思想方法原理与技巧

一、最基本原理，常用轨迹

①两点之间，线段最短；

②点到直线的距离，垂线段最短；

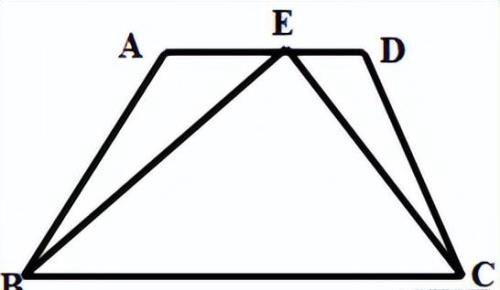
例1、如图所示，设l=AB+AD+CD，m=BE+CE，n=BC ，试比较l，m，n的大小，并说明理由

解：由题B到C的距离，根据两点之间线段最短有：AB+AD+CD>BE+EC>BC

例2、如图，在矩形ABCD中，AB=4，BC=3，点P是BC边的中点，点E、F分别是线段AC、AB上的动点，连接EP、EF，求EP+EF的最小值。

解：折叠△ABC，点B对应点N，点P对应点Q，

连接EQ则有EP=EQ

连接FQ，并过Q作QM⊥AB于点M

则有EP+EF=EQ+EF≥QF≥QM

易证△ADG≌△CNG

设DG=x，则AG=4-x

二、三角形中

①同一个三角形中，大角对大边，小角对小边；

②同一个三角形中，任意两边之和大于第三边，任意两边之差小于第三边；

思想方法：在利用三角形三边关系证明线段不等关系时，如果直接证不出来，可连接两点或延长某边构造三角形，使结论中出现的线段在一个或几个三角形中，再利用三边关系定理及不等式性质证题。

例3、如图，D，E是△ABC内两点，求证：AB+AC＞BD+DE+CE

证明：两边延长线段DE，分别交AB、AC于点F、G，则有

AB+AC=AF+FB+AG+GC

=AF+AG+FB+GC

＞FG+FB+GC

=FD+DE+EG+FB+GC

=FD+FB+DE+EG+GC

＞BD+DE+CE

∴AB+AC＞BD+DE+CE

例4、已知：P为△ABC内任一点，求证：（AB+BC+AC）/2 < PA+PB+PC < AB+BC+AC

证明：先证左边

AB<PA+PB

BC<PB+PC

AC<PA+PC

以上三式左右两边相加得：

AB+BC+AC＜2(PA+PB+PC)

即（AB+BC+AC）/2＜PA+PB+PC

再证右边

由大角对大边,可知：

在△APB中，PA<AB

在△BPC中，PB<BC

在△APC中，PC<AC

以上三式左右两边相加得：PA+PB+PC＜AB+BC+AC

∴1/2（AB+BC+AC）＜PA+PB+PC＜AB+BC+AC

三、圆

①同圆或等圆中，所有弦，直径最长；

②同弧或等圆中，大弦或大圆心角所对的弦心距小，小弦或小圆心角硕对的弦心距大；

思想方法：几何最值问题中不外乎“将军饮马”、“造桥选址”等几种比较经典的模型，解决的基本上是线段和最小问题，但解决最大值时“直径”就有妙用了！

注意：定角对定边角顶点的轨迹是该三角形的外接圆

好了，今天的内容就分享到这里，如果您有疑问，可以在文章下方留言，欢迎继续关注，精彩还将继续！

本文内容由小姿整理编辑！