角平分线问题七大模型(角平分线的经典题型)

导语：吃透《角平分线常见解题模型》，轻松搞定中考几何题

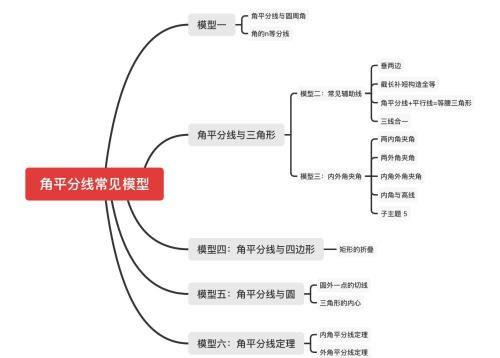
【知识梳理】角平分线作为图形最基础的概念，在选择题、填空题和几何证明题中屡见不鲜，同学们除了掌握角平分线的概念和性质定理以外，还需要对常见的角平分线的模型进行了解，在与平行线、三角形、四边形、圆等背景知识的基础上，结合角平分线得到一些常见的结论并对此进行整理记忆。

对此将角平分线的常见模型分为如下六个模块，其中前五模块为基础模块，需要同学们掌握其中结论的证明步骤,第六模块为补充模块，只需要了并会运用即可。

模型一： 角分线与圆周角和角的n等分线

①角分线与圆周角

模型分析： 如图，直线AB、CD相较于点O，OE⊥AB于点O，OF平分∠AOE，∠1=15°30’，则下列结论不正确的是（ ）

【解析】解：A、∠AOD与∠1互为补角，说法正确；

B、∠1的余角：90°-15°30′=74°30′，说法正确；

C、∵OE⊥AB，

∴∠AOE=90°，

∵OF平分∠AOE，

∴∠2=45°，说法正确；

D、∠DOF=180°-45°-15°30′=119°30′，原题说法错误；

故选：D．

解题通法：掌握余角,补角,角平分线,垂线的性质,通过加减运算解决问题

模型精练：

②角的n等分线

模型②分析：

模型②精练：

模型二： 角平分线与三角形(常见辅助线构造全等三角形)

①垂两边模型分析：

②截长补短构造全等三角形

③角平分线+平行线=等腰三角形

模型分析： 由平行线得到内错角相等,由角平分线得到相等的角,等量代换进行解题.

解题通法： 平行线与角分线组合在一起会得到等腰三角形.

④三线合一(中垂线)

解题通法： 角平分线、高线、中线其中两者重合时也能得到另外的一条件，即此时三线合一，角平分线的所有性质均可使用。

模型三:内外角平分线的夹角

①两内角平分线的夹角

解题通法: 三角形两内角的平分线的夹角等于90°与第三个内角的一半的和．(当两直线平行时,同旁内角的角分线夹角=90°)

解题通法:矩形的翻折遵照着图形对称的原则,折痕就是对称轴,即角平分线所在的直线,;矩形的翻折中默认存在直角,这一结论在求角度时常结合两锐角互余,当在求边的长度是常结合勾股定理求解.

解题通法:用HL证明直角三角形的全等,由全等的性质得到角平分线,这一过程也说明角平分线上的点到角两边的距离相等.

解题通法:三角形的内心通常结合三角形的面积与周长一起考查,常常通过角平分线性质定理得到半径相等作为突破口,结合面积公式求解.

解题通法: 三角形内角平分线分对边所成的两条线段，和两条邻边成比例．

解题通法: 三角形两边之比等于其夹角的外角平分线外分对边之比

本文内容由小熊整理编辑！