要求梯形的面积(求出下列梯形的面积)

导语：这道题要求梯形面积，但无法使用公式，这些知识点才是解题关键

今天，数学世界给大家分享一道小学数学中求图形面积的题，这道题难度不大，并不需要作辅助线。解决此题关键是要灵活运用等底等高的三角形的面积相等，等高不等底的三角形的面积比等于其对应底的比，掌握了这些知识，此题做起来就比较容易了。下面，我们就一起来看这道例题吧！

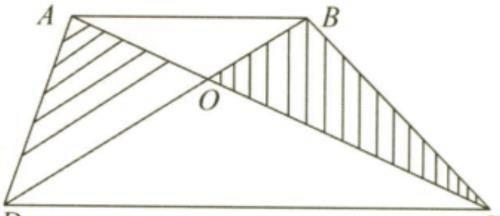
例题：（小学数学题）如图，已知在梯形ABCD中，AB为上底，CD为下底，如果阴影部分的总面积是12平方厘米，三角形COD的面积是18平方厘米，求梯形ABCD的面积是多少平方厘米？

分析：此题与我们见到的一般题目不同，题中直接告诉了阴影部分的面积，而要求的是整个图形的面积，但是不管怎么变化，这类题型的解题思路变化不大。由图可知：三角形ADC和三角形BDC等底等高，则它们的面积就相等，若分别减去公共部分（即三角形DOC），则各自剩余的部分面积也相等，即两个阴影三角形的面积相等。因为阴影部分的总面积是12平方厘米，所以其中一个阴影三角形的面积就是6平方厘米。

由于三角形COD的面积是18平方厘米，三角形AOD的面积是6平方厘米，根据“等底不等高的三角形的面积比等于其对应底的比”可以得出AO：OC=1：3，同样可以推出，三角形AOB和三角形BOC的面积比也是1：3，由此可以求出三角形AOB的面积，梯形的面积就等于四个三角形的面积之和，于是问题得解。

解：因为三角形ADC和三角形BDC等底等高，再分别减去公共部分（即三角形DOC），

所以S△ADO=S△BOC=12÷2=6（平方厘米），

根据“等底不等高的三角形的面积比等于其对应底的比”，

得AO：OC=6：18=1：3，

同理S△AOB：S△BOC=1：3，

所以S△AOB=6÷3=2（平方厘米）

梯形ABCD的面积是2+12+18=32（平方厘米）

答：梯形ABCD的面积是32平方厘米。

由于时间仓促，若文中出现一些小错误，还请大家谅解！郑重声明：这里全部文章均由猫哥原创，“数学世界”专注小学和初中数学知识分享。若朋友们还有不明白的地方或者有更好的解题方法，欢迎留言参与讨论。

本文内容由小开整理编辑！