中考数学抛物线与几何问题(为什么吃他汀类药物不能吃柚子)

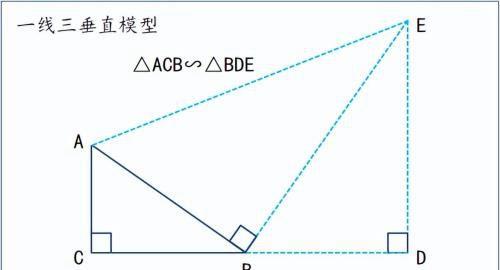
导语：中考几何压轴 30 几何与函数 抛物线中倍角模型 三垂直 以及12345模型

中考几何压轴 30 几何与函数 抛物线中倍角模型 三垂直 以及12345模型

这一系列，不限专题，解析系列经典几何题，提高几何分析解决问题能力。

题33. 《倍角点坐标》

已知抛物线G过A(-1.0)、B(4,0)、C(0.2)三点，D是第一象限内抛物线上一点，DE⊥BC于E。如果∠CDE＝2∠ABC，求D点的坐标。

〖一般性提点〗

[1]. 在二次曲线几何综合类题型中，一线三直角是频度较高的辅助线手段。

要问为什么，大概是有直角坐标系的缘故，特别是二次函数与坐标轴有三个交点时（y轴必有一个，x轴交点个数则取决于判别式），这些交点至少构成了两个直角三角形。

[2]. tanα＝1/2，tan2α＝4/3，tanβ＝1/3，tan2β＝3/4。几何证明来自特殊Rt三角形：勾3股4弦必5。

当然，若熟悉正切倍角公式，三角证明简洁而抽象。

这个模型辅助你在特殊条件下，快速计算相关角度的正切值，或者辅助迅速判断题设Rt三角形的形状（三边之比）。

[3]. 求抛物线上点的问题，一般方法是根据题设求出该点所在直线方程（或一次函数），然后与抛物线方程联立求解交点坐标。

[4]. 也有设交点坐标为(m, f(m))，然后根据题设和几何原理，找到m所满足的方程并求解m。这里得到的方程和[3]中消去y后的方程应该是一样的。

重新写下题设，方便阅读。

已知抛物线G过A(-1,0)、B(4,0)、C(0,2)三点，D是第一象限内抛物线上一点，DE⊥BC于E。如果∠CDE＝2∠ABC，求D点的坐标。

〖题目分析〗

[1]. 抛物线方程

设抛物线V：y＝a(x＋1)(x－4)，又经过C(0,2)：a＝-1/2，得

V：y＝-(1/2)x²＋(3/2)x＋2

计算一下顶点坐标，便于画出题解图：(3/2,25/8)。

[2]. 构造三垂直结构

本题关键在依据题设倍角关系，求出CD所在直线L的方程。若能在L上找到一点G，易求其坐标，则目标就可实现。

为此构造三垂直结构：

过B作BG⊥BC交直线L于G，作GF⊥x轴于F。

角度分析如图所示。易知△BFG∽△COB。

利用相似和倍角关系，可求出G点坐标。

在Rt △COB中，求得BC＝2√5；

tanθ＝1/2；

☞ tan2θ＝4/3；

☞ 在Rt △CBG中，BG＝(3/4)BC

得BG＝(3/2)√5；

☞

在Rt△BFG中，设BF＝λ，则GF＝2λ，由勾股定理求得λ＝3/2，即

BF＝3/2，GF＝3；

☞ 由此解得G点坐标G(11/2,3)

[3]. CD所在直线L的方程

斜率k：过C(0,2)和G(11/2,3)

∴ k＝(3－2)/(11/2－0)＝2/11；

L：y＝(2/11)x＋2.

[4]. 求交点D

解联立方程：

V：y＝-(1/2)x²＋(3/2)x＋2

L：y＝(2/11)x＋2

得x＝0（舍），或x＝29/11，

相应的 y＝(2/11)×(29/11)+2

y＝300/121,

D(29/11, 300/121).

本文内容由小心整理编辑！