程序设计中类是什么(类是程序的基本单元)

导语：用程序设计中“类”的概念来理解本体论中的“存在”

在哲学本体论研究中，主要研究对象是“存在”或“是”。由于“存在”的概念过于抽象，千百年来哲学家门都在苦苦追寻其本质，并争论至今。

关于“存在”的研究资料非常多，各种观点不一而足，这里就不在赘述。虽然“存在”是一个纯粹抽象的概念，它只能存在于人的思维当中，但是在这里仍然想借助程序设计中“类”的概念来试着比喻“存在”这个概念。

首先简单介绍一下“类”的概念。类就是定义一类有共同属性的抽象对象，类可以一级级继承，子类完全继承父类的属性，子类只需要增加自己特有的属性进行扩展。

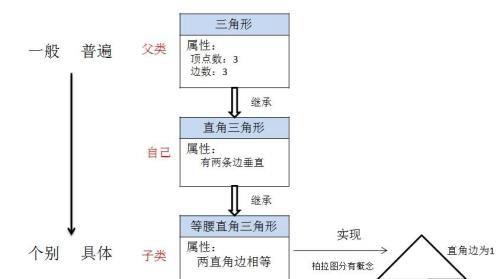
图1.中定义了一个“三角形”类，它的属性是拥有：3个顶点，3条边。再定义一个“直角三角形”类，它从父类“三角形”继承而来，继承了父类的有个顶点、3条边属性，因此只需另外规定有两条边垂直就行。同理“等腰直角三角形”继承了“直角三角形”的全部属性，只需规定两直角边相等就行了。

图 1

注：此处只做原理性描述，不一定完全符合软件设计规范，还有为了直观易懂，属性描述尽量简洁，例如三角形两条边之和大 于第三边、每个顶点只连接两条边等就不在图中说明了。

三角形、四边形、五边形等多边形有什么共同特征呢？我们可以抽取这些共同特征作为它们的父类。我们发现这些多边形共有的特点是它们都是由几个顶点和几条边组成的封闭图形，每个顶点只连接两条边并且边数和顶点数相同，这样我们可以抽象出它们的父类“多边形”类。见图 2。

图 2

注：为了方便大家理解这里采取从下至上倒推的方法来抽象出上一级类，实际编程中是从上到下一级级定义继承的。

多边形是封闭图形，我们常见的封闭图形还有圆形、椭圆等（其实圆是椭圆的特殊情况）。这些封闭图形有什么共同特征呢？我们发现它们外观不确定但是都有面积和周长，因此我们抽象出它们的父类“图形”类。见图 3。说明：“图形”类已无法实现，因为一个东西只知道有面积和周长我们不确定它是什么样子，这属于虚类。

图 3

“图形”类是封闭图形，但有些图形没有面积，比如线段和点，它们又有什么共同特点呢？我们已找不出它们的共同属性了，我们发现它们都有外观，是看得见的，因此它们都具有一个“显示”自己的功能。所有我们可以抽象出“形状”类作为它们的父类。见图 4。

图 4

“形状”类有外观，可以显示自己，而有些类没有外观，比如函数类、通讯类等，我们找不出这些类的共同属性和功能了，因此只能抽象出一个没有内容的空类为父类，我们叫作 “根”类，在程序设计中也叫纯虚类。见图 5。

图 5

图6为整体继承关系。

图 6

以上列举了类的简单继承关系。图中的“根”类没有内容或者说是空的，但是所有其它的类都从它那里派生，就像本体论中的“存在”或“是”，它是无但又蕴含着有，一起源于它又归于它，它是一切“存在者”存在的原因。

《道德经》中的“天下万物生于有，有生于无”、“无名，万物之始也；有名，万物之母也”、“道生一，一生二，二生三，三生万物”等思想也与这种从无到有的“类”的继承关系有某些相似之处，可供大家参考。

本文内容由小媛整理编辑！