抛物线方程的一般式推导(抛物线一般式是怎么来的)

导语：以一道抛物线压轴题为例探究一般性和特殊性关系

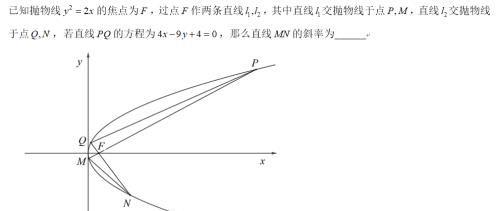
先给出题目，自己可以试着做一下，顺便也猜测一下这两条直线斜率的关系以及交点的位置。

题目是某次高三测试中填空题的压轴题，题目看上去并不难，解起来也很容易，联立PQ和抛物线可求出P,Q两点的坐标，再根据P,M；Q,N横坐标乘积为定值求出M,N的横坐标，利用斜率公式和抛物线方程化简即可，过程如下：

根据求得的斜率得知2kpq+kmn=0，在用geogebra作图的时候发现直线PQ和直线MN的交点竟然在准线上，图像如下：

难道莫名其妙的得到了一个抛物线中的二级结论？接下来换了一个抛物线和直线方程，根据图像看能够得到相同的结论，抛物线为y²=4x,P点横坐标为½，Q点横坐标为4,其余条件不变，看是否依旧满足上述结论，图像如下：

从图上看两条直线依旧交于一点，且在准线上，下面用一般性来验证一下这个结论是否正确：

在一开始的题目中A=C=4，p=1，满足斜率之间的等式关系，但这个倍数并不是定值，随着A,C,p的不同而改变，下面验证一下这两条直线的交点是否在准线上：

从以上证明一般性证明过程来看，两条直线斜率并不存在确定的倍数关系，而是随着抛物线和直线的形式变化而变化，但两条直线永远交在准线上，因此可得到以下结论：

过抛物线焦点的两条直线分别交抛物线于P,M,Q,N,则直线PQ和MN的交点在准线上。

这个题目是好久之前存着的一道题目，今天打开未处理文件夹看到这个题目，给出证明过程，解题时很多会用到类比推理，类比推理的前提是特殊性会满足一般性，但具体是不是还得亲自验证。

接下来的三次推文内容为复合函数和嵌套函数问题，之前有讲过，这里再重新细化一下。

本文内容由小媛整理编辑！