什么是正方形弦图(线条正方形)

导语：正方形特殊弦图的线段比例关系的应用

正方形特殊弦图的线段比例关系的应用

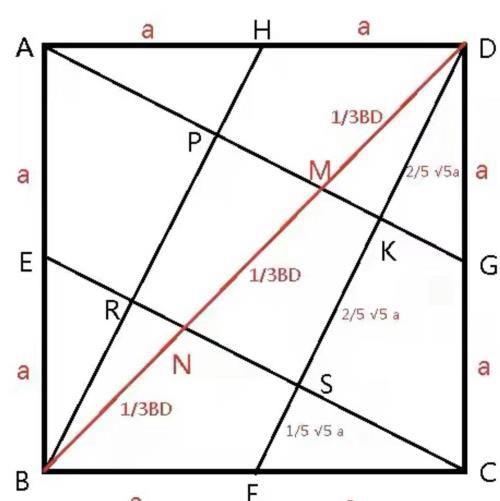
经过正方形顶点与对边中点连线构成特殊弦图（见下图），其中一些线段具有固定的比例关系，例如正方形对角线被连线均分三等份；一条连线被另外二条连线分为2份、2份和1份，即各占2/5、2/5和1/5（详见正方形弦图的几个小知识点）。利用这种比例关系我们可以快速解题，现举例如下。

题目1:（见下图）正方形ABCD中，E为BC的中点，连接DE，在DE上取点P，使AP⊥DE，连接BP，证明BA=BP。

解题思路：正方形中出现顶点与对侧中点之连线，该连线有一条垂线经过另一个顶点，我们可以联想到正方形“十”字交叉模型及其构成的弦图。延长AP交DC于F点，F点即为DC的中点。G为AD中点，连接BG后构成正方形部分弦图（见下图）。

根据上述弦图中线段比例关系，AH/HP/PF=2/2/1,H点为AP之中点。已知GB⊥AF，在三角形ABP中，BH为底边AP的垂直平分线，点B到A点和P点的距离相等，故BA=BP。

题目2：如图1，在正方形ABCD中，E是AD的中点，F是ED的中点，求证∠ABE=1/2∠CBF。

解题思路：H点和G点为AB和DC的中点，连接HD、BG和EC，HD、BG和EC分别交于M和N点，构成正方形部分弦图（见图2）。

EM/MN/NC=1/2/2，N为MC中点，EM/EC=1/5。

设EC与FB交于M´，可证明△M´EF∽△M´CB，EM´/M´C=FM´/M´B=EF/BC=1/4。

EM´/EC= FM´/FB=1/5，点M´与点M重叠。

BN为MC的垂直平分线，∠MBN=∠CBN=1/2∠CBF。

图中可证明∠ABE=∠CBN，故∠ABE=1/2∠CBF成立。

题目3：图1，正方形ABCD内有一四分之一圆弧， 圆心为正方形的一个顶点B。连接对角顶点D与其对边AB的中点M，与圆弧相交于N，求MN与ND之比？

解题思路：补全四分之一圆为半圆如图2，延长DM交CB延长线于E，因AD∥EC且M为AB中点，△MBE≌△MAD，EB=AD=BC，EC即为直径。连接CN并延长到AD，根据直径所对的圆周角为直角，故CN⊥ED，构成特殊弦图，ND占MD的2/5，MN占MD的3/5，故MN与ND之比为3/2。（另一种解法稍复杂，详见四分之一圆补全成半圆解题5例）。

延伸一下：知道以上比例关系，解下面一题就容易了。

题目如图，正方形ABCD边长为10，以A点为圆心、AB为半径作圆，E为弧DB上一点，∠DEC=135°，求△DEC的面积。（另一种解法稍复杂，详见相似三角形经典例题5例）。

题目4：在正方形ABCD中，E、F分别为AB、BC边上中点，G为线段DE上的一点，AB=10，∠EGF=45°，求DG的长？

解题思路：连接AF交ED于H，则AF⊥ED，因∠EGF=45°，所以∠HFG=45°，HG=HF。

根据前述特殊弦图中线段比例关系，设EH=x，则AH=2x，HF=HG=3x。

AF=ED=5x，DG= ED-EG=5x-4x=x=1/5 ED

ED=√5 AE=5√5

DG=√5

题目5：如图1，在等腰△ABC中，∠ABC=90°，D为BC中点，F为AC上一点，BF⊥AD，垂足为E点。证明：①AF/FC=2/1; ②∠BDA=∠CDF，∠AFB=∠CFD；③∠AEC=135°；④AE/EC=√2。

解题思路：

一、根据题意，我们补全等腰Rt三角形为正方形ABCG（图2）。延长BF交CG于H，则H为CG之中点，根据前述特殊弦图中线段比例关系，F点为正方形对角线AC的三等分点（亦可由△FCH∽△FAB来证明），AF/FC=2/1成立。

二、连接DG，可证明DG经过F点（F点均为AC、DG、BH的三等分点）。根据对称性原理，∠BDA=∠CDF，∠CFD=∠CFH；又因∠CFH =∠AFB（对顶角），故∠AFB=∠CFD。

三、D、C、H、E四点共圆（∠DEH=∠DCH=90°）。CD=CH，Rt△DCH为等腰Rt△，∠CDH=∠DHC=45°，又∠DEC=∠DHC=45°（同弦对等角），∠AEC=∠BED+∠DEC=90°+45°=135°。

四、在四边形DCHE中，设CD=CH=x，

DH=√2x，

DE=1/5 BH=1/5√5x，

EH=3/5 BH=3/5√5x，

根据托勒密定理，CD·EH+DE·CH=EC·DH，

EC=2/5√10 x。

AE/EC=(4/5√5x) / ( 2/5√10 x)= √2。

附：另有一种相对简单的方法：即证明△BDH∽△CEA。

DH/DC= DH/DB=√2。

AE/EC=√2。

本文内容由小荣整理编辑！