初中数学婆罗摩笈多模型(婆罗摩多模型数学题)

导语：第五章.轴对称模型（二十）——婆罗摩笈多模型

第五章.轴对称模型（二十）——婆罗摩笈多模型

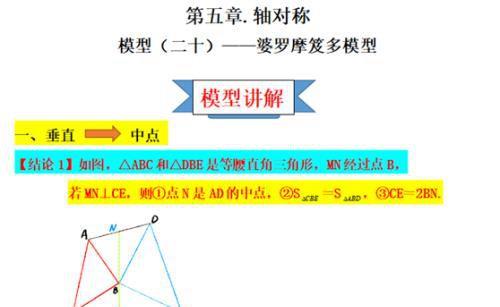
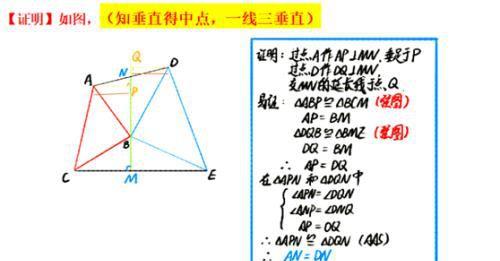
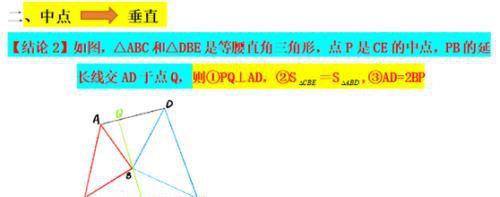
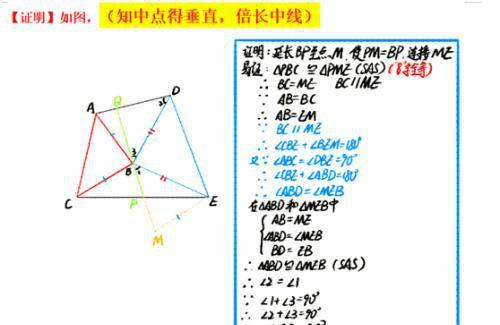
典例1 ☆☆☆☆☆

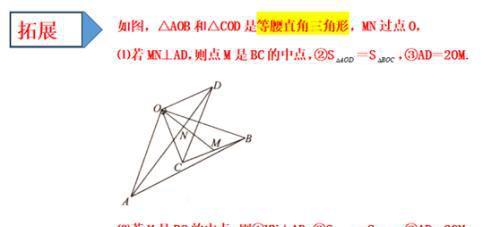
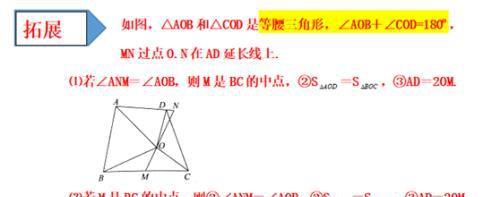
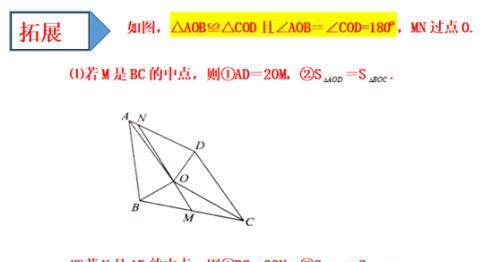
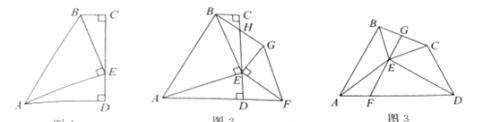
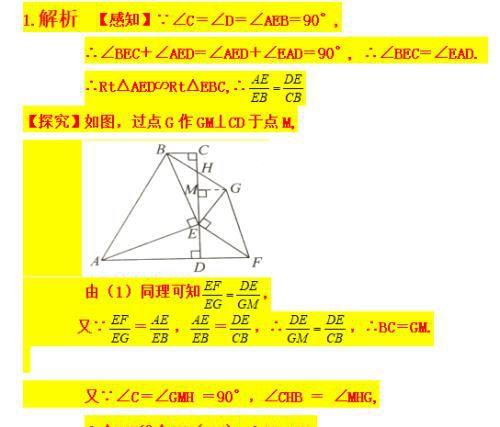
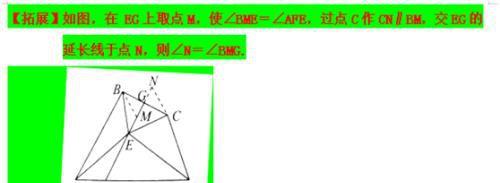
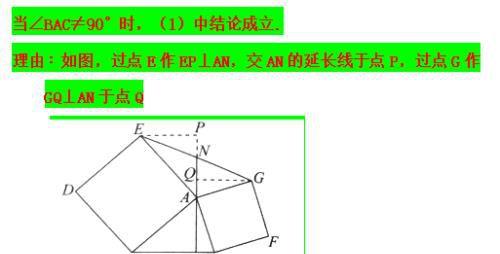
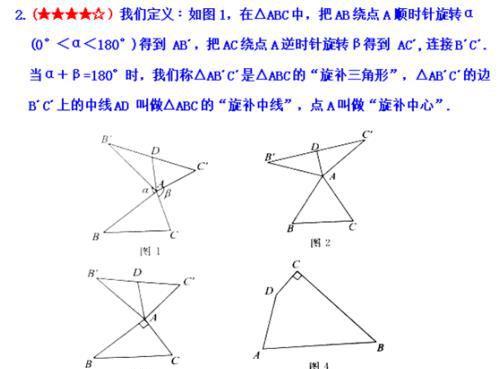
定义：如图1，在△ABC和△ADE中，AB＝AC＝AD＝AE，当∠BAC＋∠DAE＝180º时，我们称 △ABC与△DAE互为“顶补等腰三角形”，△ABC的边BC上的中线AM叫做△ADE的“顶心距”.

特例感知∶

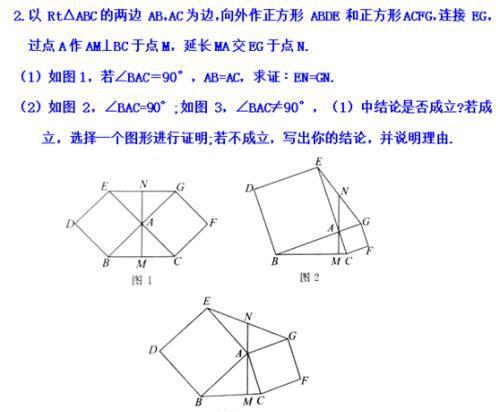
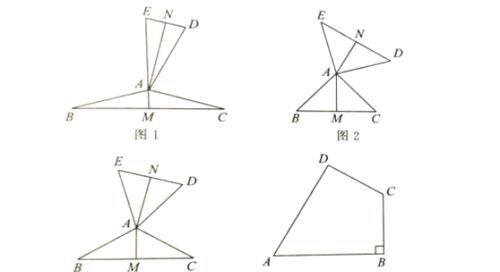
⑴在图2、图3中，△ABC与△DAE互为“顶补等腰三角形”，AM， AN 分别是“顶心距”.

①如图2，当∠BAC=90°时，AM与DE 之间的数量关系为AM=_____DE;

②如图3，当∠BAC=120°，BC=6时，AN的长为__________.

猜想论证∶

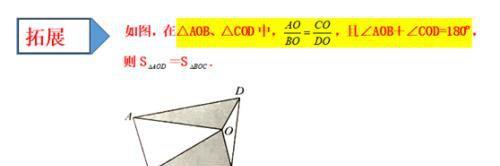
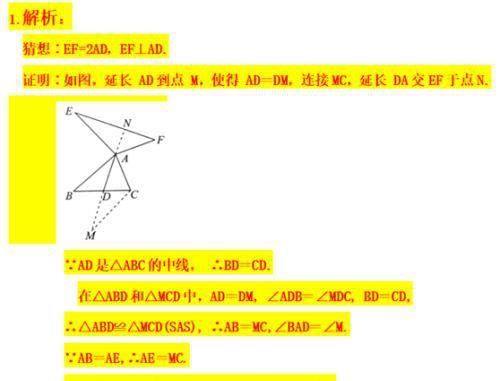
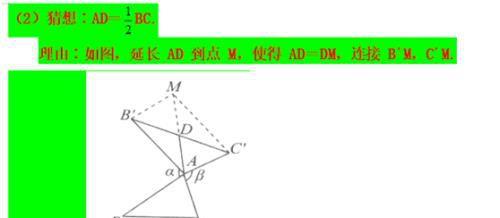
⑵在图1中，当∠BAC为任意角时，猜想AM与DE 之间的数量关系，并给予证明。拓展应用

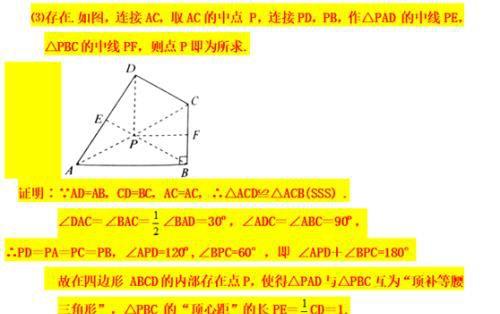
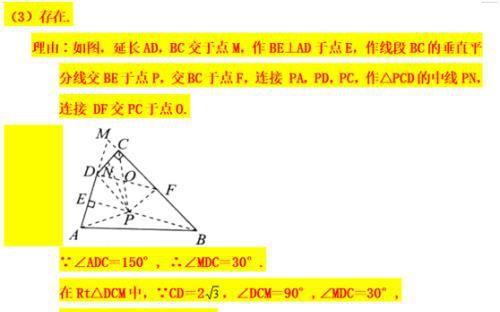
⑶如图4，在四边形ABCD中，AD=AB，CD=BC，∠B=90°，∠A= 60°，CD=2，在四边形ABCD的内部是否存在点P，使得△PAD与△PBC互为“顶补等腰三角形”?若存在，请给予证明，并求出△PBC的“顶心距”的长;若不存在，请说明理由。

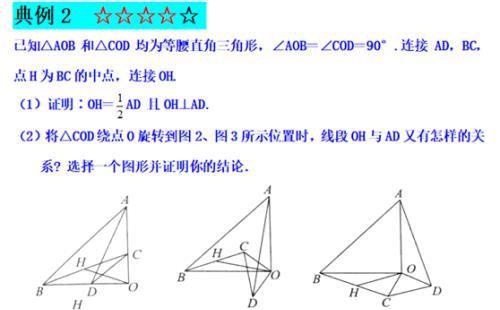
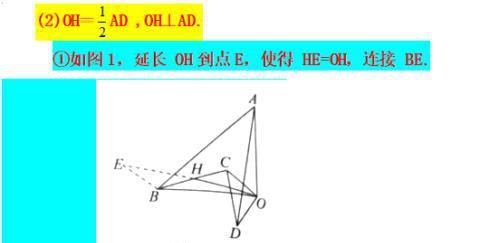
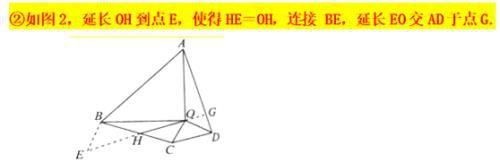
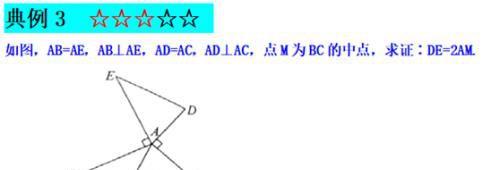
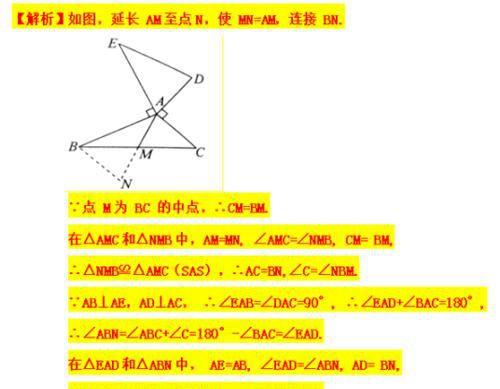
婆罗摩笈多是一个非常重要的模型，主要强调的是两个等腰直角三角形的手拉手 ，知中点证垂直 ，知垂直证中点，涉及相对应的辅助线 ，知中证垂可倍长 ，知垂证中一线三垂直，这是一个相对复杂的几何模型，需要左右两边同时去构造全等或相似.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小余创作整理编辑！