圆上动点的值问题三种解法山(圆上的动点求大值)

导语：经典的圆上动点形成角度的最值问题（一）

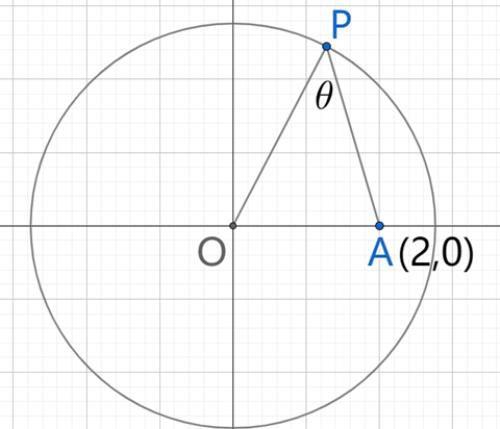
题目：圆x²+y²=8,原点为O，圆上的点A坐标为（2,0），圆上一个动点P，求∠OPA的最大值。

这道题的解题思路一定是把θ角转化为关于某个变量的表达式，进而求得最大值。这道题虽然难度不是特别大，但是有几种解法能够大大拓展解析几何的思维，有必要把每种方法琢磨透彻。这些方法都是高中数学阶段的基本方法，在解决解析几何关于圆的问题时非常有用。

最常规最直观的方法，就是设动点P坐标，然后计算夹角，再根据表达式求最大值。P是圆上的动点，又给出了圆的方程，那么可以设动点P的坐标为

这是圆上一点坐标的常用表示方法。

根据线段夹角公式可知：

其中：

代入夹角公式可以得：

化简到这个程度，现在目标是求这个关于sint和cost函数的最大值。

经过观察发现，直接求这个同时含有sint和cost的函数最大值比较困难，但这个表达式又比较简单，因此可以尝试使用设目标值转化为方程的方法进行计算。

不妨设tanθ=x，于是有：

整理可得：

对于这种同时包含cost和sint的表达式，常用的化简方法是将其视为两角和公式的展开形式，使用两角和公式对其进行整合，形成一个角的三角函数，计算如下：

（PS：这种化简方法是高中数学最常用也是最基本的化简方法，将正弦余弦的系数视为某个角度的正弦和余弦值，从而利用和差化积公式整合成一个角的三角函数。）

于是有：

两边平方可以求得：|x|≤1

取最大值时，tanθ=|x|=1，即θ=45°

本文内容由小珊整理编辑！