整式的运算中考题(中考整式计算题及答案)

导语：数学中考第一轮复习知识点（整式运算）

一、单项式及多项式

【高频考点精讲】

1．单项式乘单项式

单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。注意：在计算时，应先进行符号运算，积的系数等于各因式系数的积；

2．单项式乘多项式

（1）单项式与多项式相乘的运算法则：单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加。

（2）注意事项：

①单项式与多项式相乘实质上是转化为单项式乘以单项式；

②用单项式去乘多项式中的每一项时，不能漏乘；

③注意确定积的符号。

二、整式混合运算

【高频考点精讲】

1．有乘方、乘除的混合运算中，要按照先乘方后乘除的顺序运算，其运算顺序和有理数的混合运算顺序相似；

2．“整体”思想在整式运算中较为常见，适时采用整体思想可使问题简单化，并且迅速地解决相关问题，此时应注意被看做整体的代数式通常要用括号括起来。

三、幂的运算

【高频考点精讲】

（1）同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加。

am•an＝am+n（m，n是正整数），拓展：am•an•ap＝am+n+p（m，n，p都是正整数）

（2）幂的乘方法则：底数不变，指数相乘.

（am）n＝amn（m，n是正整数）

（3）积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘．

（ab）n＝anbn（n是正整数）

（4）同底数幂的除法法则：底数不变，指数相减．

am÷an＝am﹣n（a≠0，m，n是正整数，m＞n）

四、完全平方公式及其几何背景

【高频考点精讲】

1．完全平方公式

（1）（a±b）2＝a2±2ab+b2；

（2）特征：

①左边是两个数的和的平方；

②右边是三项式，其中首末两项分别是两项的平方，为正，中间一项是两项积的2倍；符号与左边的运算符号相同。

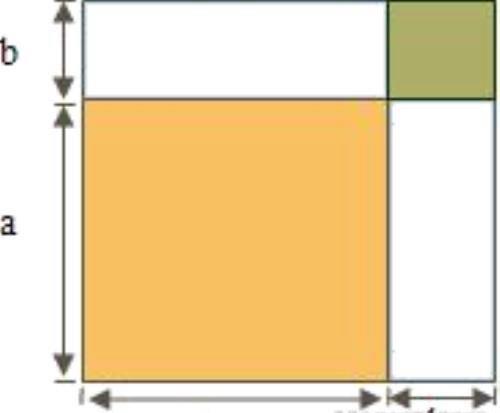
2．验证完全平方公式的几何图形

（a+b）2＝a2+2ab+b2．（用大正方形的面积等于边长为a和边长为b的两个正方形与两个长宽分别是a，b的长方形的面积和作为相等关系）

五、平方差公式及其几何背景

【高频考点精讲】

1．平方差公式

（a+b）（a﹣b）＝a2﹣b2

（2）特征：

①左边是两个二项式相乘，并且这两个二项式中有一项完全相同，另一项互为相反数；

②右边是相同项的平方减去相反项的平方；

2．验证平方差公式的几何图形

本文内容由小梓整理编辑！