任意可数集的所有有限子集构成的集族是可数集族(任意多个可数集之并可数)

导语：数学奇谈：任意可数集E，必然存在实数a，使得E与E+a不相交

当康托引入集合概念以后，有许多超出我们想象的性质不断被挖掘。比如下题：

对实数轴上任意可数集E，存在实数a，使得E∩（E+｛a｝）是空集。

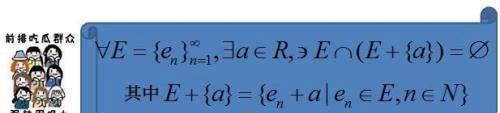
完全使用数学符号，就会变得像天书一样

E有无穷多个元素，但仍然可以巧妙的与E+｛a｝擦肩而过。是不是很神奇？

证明：反证法，假设任意点a，E∩（E+｛a｝）不是空集。那么这两者的交集中至少包含一个元素，不妨记做ei。于是必然存在E中另一个元素ej，使得ei=ej+a。

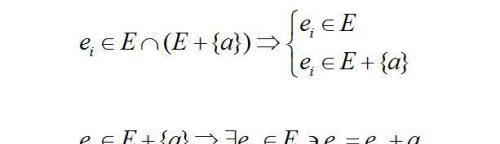
注意到a是从R中任意取定的，则上面的结论意味着“R中所有的点都可以由E中某两个点作差获得”，这个结论对吗？这就涉及到集合势的比较。我们构造点集如下

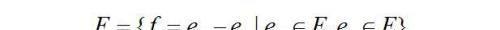
那么F的势与集合E×E的势相同，都是可数集。但是R是不可数集，所以一定存在a∈R，使得E∩（E+｛a｝）是空集。

Cantor，1845.3.3-1918.1.6，德国数学家，集合论的创始人

题外话，康托活着的时候，集合论受到一些大数学家的打压，其本人最终在精神病院度过余生。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小畅创作整理编辑！