几何中的定值问题(解析几何定值定点例题)

导语：几何定值问题：综合练习题5例

几何定值问题：综合练习题5例

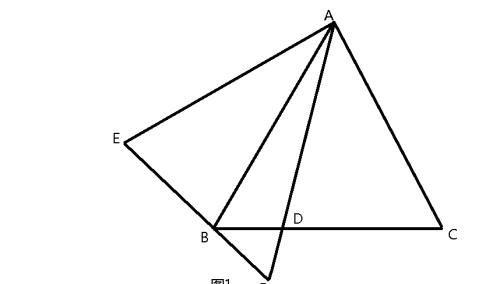
题目1：在△ABC中，AB=AC，D为BC上任意一点（非中点），E是点C关于AD的对称点，EB与AD相交于点F。求证AD·AF的值与D点的选择无关。

解题思路：本题欲证明两条线段AD·AF的值为一定值，应与已知三角形ABC的边长、高等要素有关，结合图形，首先想到用相似三角形解决问题，尤其是母子相似三角形模型，在△ADB和△ABF，已知∠BAF为公共角，如果能证明∠ABD=∠AFB则两个三角形相似。

图2所示，连接ED、FC，根据已知条件，则四边形AEFC为轴对称图形，对称轴是AF，可知A、E、B、D和A、B、F、C四点共圆，这样∠α=∠β，由此得出：

∠ABD=∠AFB，△ADB∽△ABF，

AF/AB=AB/AD,

AD·AF=AB²,为定值， AD·AF的值与D点的选择无关。

题目2：如图，在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D，点E是AC边上任意一点（不含端点），AF⊥BE于点F，交BC于点G，求∠DFG的度数（45°）。

解题思路：将等腰Rt△ABC补全成大正方形，再补全成弦图形成中间小正方形，D点即为两个正方形的中心，DF即为小正方形对角线的一部分，故∠DFG =45°，为定值。另一种解法见初中几何定值问题：定角5例

题目3：如图，已知半径为R的圆O及弦AB，P为圆O上任意一点，PA、PB分别交AB的中垂线于E、F。求证OE·OF为定值。

本题求证OE·OF为定值，解题思路同题目1，应用相似三角形求解；与圆相关的定值一般要考虑与半径或直径相关。具体解法详见圆弧、圆周角及圆心角应用题5例

题目4：如图,△ABC是边长为1的等边三角形,△BDC是顶角BDC 为120°的等腰三角形，以D为顶点作一个60°角,角的两边分别交AB于M,交AC于N,连接MN,形成一个三角形，来证：△AMN的周长等于2。

解题思路：采用类似正方形半角模型的旋转方法或截长补短法，延长AB至E点，使BE=NC，则Rt△NCD≌Rt△EBD（Rt△NCD绕D点逆时针旋转120°亦可），NC=BE，ED=ND，∠α+∠θ=60°，MD=MD，

故△MND≌=△MED，MN=ME=MB+NC。

△AMN的周长=AM+AN+MN= AM+AN+ MB+NC

=（AM+MB）+（AN+NC）

=AB+AC

=2,为定值。

题目5：如图1所示，在四边形ABCD中，△ABD是正三角形，∠BCD=120°，BC=CD，点E、F分别在BC、CD边上。∠EAF=30°， AE，AF分别交BD于M、 N。

(1)求BE、EF、FD的关系；（2)若CE=2，CF=1，求MN的长度；(3)连接EN、FM交于G，求证AG⊥EF。

解题思路：(1)求BE、EF、FD的关系。

类似题目4，采用旋转方法或截长补短法，证明EF=BE+FD（图2）。

（2)若CE=2，CF=1，求MN的长度。

图2示，∠α+∠θ=180°-30°=150°，

∠AFE=∠α=150°-∠θ，

∠AMN=∠BME=150°-∠θ，

∠AFE=∠AMN，

△AMN∽△AFE，其相似比等于对应边高之比（图3）。

其中AO=√3/2 BD，AH=AB=BD，AO/ AH=√3/2。

MN/EF= AO/ AH=√3/2。

EF通过勾股定理可求出，MN值可得。

(3)连接EN、FM交于G，求证AG⊥EF。

见图4，在四边形AMFD中，∠MAF=∠MDF=30°，故A、M、F、D四点共圆，则AM⊥MF；同理，EN⊥AF，

在△AEF中，G点则为其垂心，故连接AG并延长交EF比为其高，AG⊥EF成立。

本文内容由小蔼整理编辑！