数形结合的巧妙解法(数形结合的意思是什么)

导语：经典再现13——数形结合 妙不可言

题：已知实数a、b满足0<a<1，0<b<1，且a√(1-b2)+b√(1-a2)=1，求证：a2+b2=1.

本题虽然有多种证法，但如果从数形结合思想出发，由已知等式的左边联想到托勒密定理——圆内接四边形两组对边的乘积之和等于对角线的乘积，构造圆内接四边形则可得一种令人拍案叫绝的巧妙证法。

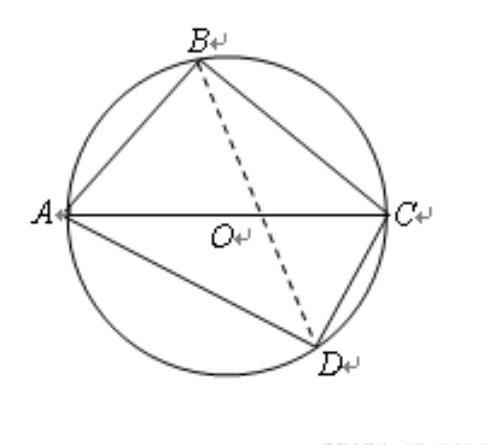
证明：如图，设AC=1，以AC为作直径作⊙O，在⊙O上AC的两侧分别作弦AB=a，AD=b，连接BC、DC。

因为AC为直径，

所以∠B=∠D=90°，

所以BC= √(1-a2)，DC= √(1-b2)。

连接BD。

因为四边形ABCD是圆内接四边形，

所以由托勒密定理，得

AB·DC+AD·BC=AC·BD，

即a√(1-b2)+b√(1-a2)=BD，

因为a√(1-b2)+b√(1-a2)=1，

所以BD=1，

所以BD是⊙O的直径，

所以∠BAC=90°，

所以AB2+AD2=1，

即a2+b2=1.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小春创作整理编辑！