求正方形阴影面积公式(求正方形阴影部分面积六年级技巧)

导语：求阴影面积问题：正方形和矩形并排放，求绿色部分面积是多少。

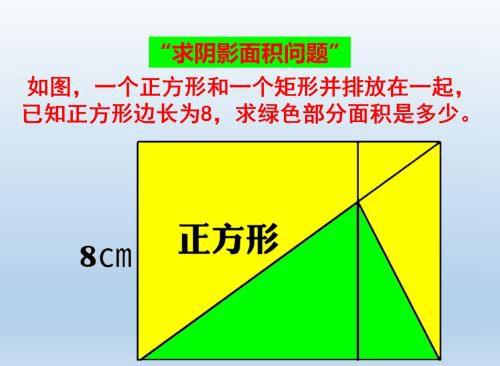
题目：如图，一个正方形和一个矩形并排放在一起，已知正方形边长为8，求绿色部分面积是多少。

解法1：最直接的方法是把矩形内阴影三角形变形，把矩形内三角形的高变成底，把底变成高，这时与正方形内阴影△组成了一个底和高都是8的三角形阴影三角形

解法2：连接正方形的对角线（绿色部分的上面这个），正好与矩形的小三角形组成一个钝角三角形，它的面积正好是矩形的一半，而矩形中的绿色部分面积正好是正方形中对角线的小空白面积。故绿色面积为8×8÷2＝32

解法3：作正方形、矩形两条对角线，经过等积对换，可知阴影面积等于正方形面积之半。（即把矩形右下角顶点通过两次拉窗帘，先向上拉至矩形右上角顶点，再向左拉至正方形右上角顶点，构成半个正方形的三角形。）S阴＝8×8÷2＝32

解法4：正方形一半连接正方形右下定点和长方形右上点。可以把阴影看成两个三角形。右边的三角形就等于以他为底连接辅助线构成的三角。

解法5：两次拉窗帘，变成半正方形 从长方形右下角拉到右上角，再拉到正方形右上角 S阴影＝8×8／2＝32（c㎡）

本文内容由小蔼整理编辑！