求多面体体积的技巧(高中多面体面积和体积公式)

导语：一道高中立体几何题-求多面体的体积

一道高中立体几何题-求多面体的体积

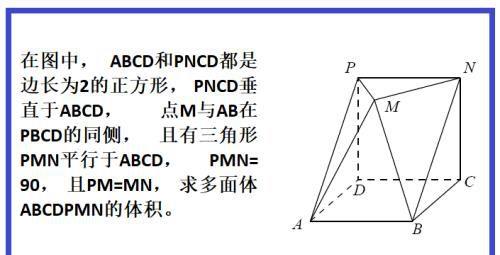
在图中， ABCD和PNCD都是边长为2的正方形， PNCD垂直于ABCD， 点M与AB在PBCD的同侧， 且有三角形PMN平行于ABCD， PMN=90， 且PM=MN， 求多面体ABCDPMN的体积。

解：多面体ABCDPMN显然是由两个多面体组合而成，一个是PAD-NBC组成的三棱柱，另一个是由点M和底面PABN形成的M-PABN所组成的椎体。

对于第一个多面体由于是三棱柱，其底面面积为2x2/2=2, 而棱柱的高为2， 所以有体积

V1=Sh=2x2=4,

下面求第二个多面体棱锥的体积，这个棱锥的底面为PABN， 其两个边可以求出为：

PN=2， BN=2√2

所以底面PABN的面积=2x2√2=4√2

下面求棱锥的高

如图做MT垂直于PN，

在直角三角形MPN中斜边的高MT=1， 这点可以通过下图求出，

根据下图做MT垂直PN， TR垂直DC，取S是AB的中点，

因为三角形NCB全等于三角形TRS，所以∠CNB=∠RTS=45°但∠MTR=90°

所以∠MTS=90°-45°=45°

单独把三角形MST画出：

根据上图可以求出四棱锥的高h=(√2)/2

因此四棱锥的体积V2=Sh/3=4√2x(√2)/2x1/3=4/3

所以组合多面体的体积V=V1+V2=4+4/3=16/3

本文内容由小春整理编辑！