求异面直线所成的角常用的方法：

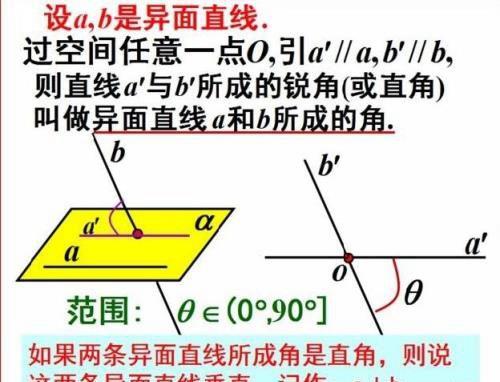
通过平行移动直线，把异面问题转化为相交直线的夹角，体现了化归思想.

（1）直接平移法， 利用图中已有的平行线平移；

（2）利用特殊点(线段的端点或中点)作平行线平移，如中位线平移（图中出现了线段的中点时）

（3）补形平移法.

判定空间两条直线是异面直线的方法

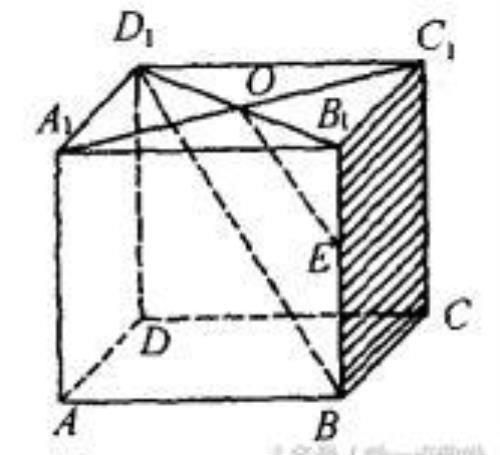
(1)判定定理：平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线.

(2)反证法：证明两线不可能平行、相交或证明两线不可能共面，从而可得两线异面.

求异面直线所成角的三个步骤

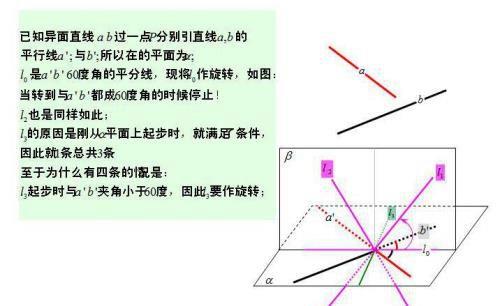
①作：通过作平行线，得到相交直线的夹角.

②证：证明相交直线夹角为异面直线所成的角.

③求：解三角形，求出作出的角，如果求出的角是锐角或直角，则它就是要求的角，如果求出的角是钝角，则它的补角才是要求的角.

易错防范

1.异面直线易误解为“分别在两个不同平面内的两条直线为异面直线”，实质上两异面直线不能确定任何一个平面，因此异面直线既不平行，也不相交.

2.直线与平面的位置关系在判断时最易忽视“线在面内”.

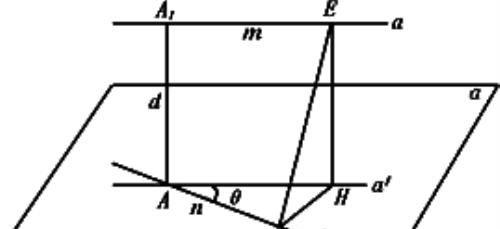
3.两异面直线所成的角归结到一个三角形的内角时，容易忽视这个三角形的内角可能等于两异面直线所成的角，也可能等于其补角.

我是【学一点数学】，欢迎评论、点赞！或关注我私聊，与你分享高考提分策略，涨分秘籍，纯干货。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小纳创作整理编辑！