中考数学动点运动中的定值问题题目(动点定义)

导语：中考数学：动点运动中的定值

图形变换及动点在运动过程中，是否存在某些变量之间的数量关系始终为定值，转化思想是解决问题的关键。

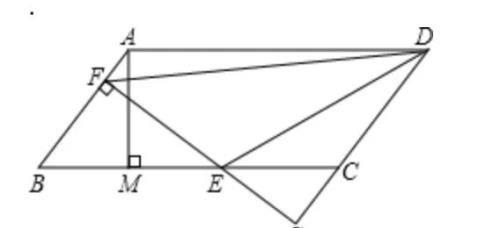
例1.如图，▱ABCD中，AB=5，BC=10，BC边上的高AM=4，E为BC边上的一动点(不与B、C重合)，过E作直线AB的垂线，垂足为F，FE与DC的延长线交与点G，连接DE，DF，△BEF与△CEG的周长之和是否为定值？如果是定值，求出这个值；如果不是说明理由。

分析：过点B作BH⊥CD，交DC延长线于点H，将两个三角形周长和转化为：BC+FG+CH

易得：四边形BHGF为▱

∴BH=FG，BF=HG

∵S▱ABCD=AB.FG=BC.AM

5.FG=40⇒FG=8

∴BH=FG=8

Rt△BHC中：CH²=10²−8²=6

∴C△BEF+C△CEG=BC+FG+CH

=6+8+10=24。

例2.矩形ABCD中，AD=8，将矩形ABCD折叠，使得点B落在CD边上的点P处

(1)如图1，已知折痕与BC交与点O，连接AP、OP、OA，若△OCP与△PDA的面积比为1:4，求CD

分析：一线三角易证：△OCP～△PDA

∵S△OCP：S△PDA=1:4

∴PC/AD=OC/PD=1/2

∴PC=1/2.AD=4，

设：CD=AB=AP=x，则：PD=x−4

Rt△ADP中：，8²+(x−4)²=x²

解得：x=10，即：CD=10。

(2)如图2，在(1)的条件下擦去AO，OP，连接BP，动点M在线段AP上(点M不与点P、A重合)，动点N在线段AB的延长线上，且BN=PM，连接MN交PB于点F，作ME⊥BP于点E，当M、N在移动过程中，线段EF的长度是否变化？若变化，说明变化规律，若不变，求出EF长度。

构造全等三角形，转化线段

分析：作MQ∥AN，交PB于点Q，

由(1)问得：AB=AP

∴△PMQ为等腰三角形，QM=PM

∵ME⊥BP

∴EQ=1/2.PQ(三线合一)①

∵BN=PM，∴QM=BN

易证：△QMF≌△BNF

∴QF=BF=1/2.BQ②

∴EF=EQ+QF=1/2.PQ+1/2.BQ=1/2.PB③

由(1)问得：PC=4，BC=8

∴Rt△PBC中：PB²=4²+8²

∴PB=4√5

即：EF=1/2.PB=2√5。

本文内容由小林整理编辑！