旋转矩阵怎么计算(旋转矩阵原理及公式)

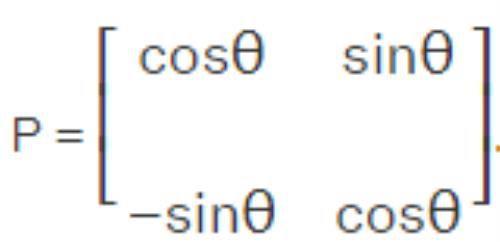
导语：旋转矩阵学习笔记，分享给大家

旋转矩阵是一种变换矩阵。该矩阵的目的是在欧几里得空间中执行向量的旋转。几何为我们提供了四种类型的变换，即旋转、反射、平移和调整大小。此外，变换矩阵使用矩阵乘法的过程将一个向量转换为另一个向量。当我们想要改变向量的笛卡尔坐标并将它们映射到新坐标时，我们会借助不同的变换矩阵。

如果我们在二维空间中工作，那么旋转矩阵的阶数将是 2 x 2。类似地，旋转矩阵在 n 维空间中的阶数是 nx n。旋转矩阵描述对象或向量在固定坐标系中的旋转。这些矩阵广泛用于在物理、几何和工程中执行计算。在本文中，我们将深入研究 2D 和 3D 空间中的旋转矩阵，并了解它们的重要属性。

什么是旋转矩阵？

旋转矩阵可以定义为对向量进行运算并产生旋转向量的变换矩阵，使得坐标轴始终保持固定。这些矩阵将向量沿逆时针方向旋转角度 θ。旋转矩阵始终是具有实体的方阵。这意味着它将始终具有相同数量的行和列。此外，旋转矩阵是行列式等于 1 的正交矩阵。假设我们有一个方阵 P。那么 P 将是一个旋转矩阵当且仅当 且 |P| = 1。

旋转矩阵示例

假设我们有一个矩阵

2X2方阵

因此，

现在，

因此，P 是一个旋转矩阵。我们可以说，P 相对于二维系统中的 x 将笛卡尔坐标沿逆时针方向旋转 θ。

二维推导中的旋转矩阵

设 G 是 xy 平面中长度为 r 的向量，它与 x 轴形成角度 v。我们现在将 G 逆时针旋转角度 θ。如果 (x, y) 是向量 G 点起点为原始坐标，那么 (x&39;) 将是旋转后的新坐标。

我们用极坐标形式表达G (x, y)；

x = r cos v —— (1)

y = r sin v —— (2)

类似地，以极坐标形式表示 G&39;, y&39; = r cos (v + θ)

y&39; = r (cos v.cos θ - sin v.sin θ)

= r cos v.cos θ - r sin v.sin θ

从（1）和（2）我们有:

x&39; = r (sin v.cos θ + cos v.sin θ)

= r sin v.cos θ + r cos v.sin θ

y&39;，y&39;），我们遵循以下公式：

假设一个物体绕所有三个轴旋转，那么这样的旋转矩阵将是上述三个旋转矩阵的乘积

[P (z,α), P (y,β) 和 P (x,γ)]。一般的旋转矩阵表示如下：

为了找到旋转向量关于所有三个轴的坐标，我们将旋转矩阵 P 与向量的原始坐标相乘。

3D 推导中的旋转矩阵

为了推导 x、y 和 z 旋转矩阵，我们将遵循类似于推导 2D 旋转矩阵的步骤。3D 旋转由角度和旋转轴定义。假设我们将坐标 (x, y, z) 给定的点 Q 关于 x 轴移动到由 (x&39;z&39;, y&39;, y&39;) = (5, -2, -6)答案： (5, -2, -6)

本文内容由小奈整理编辑！