辅助线初中几何(初中几何常见辅助线口诀)

导语：中考几何压轴 70 辅助线法则 弦长与直径的关系

中考几何压轴 70 辅助线法则 弦长与直径的关系

这一系列，不限专题，解析系列经典几何题，提高几何分析解决问题能力。

题77. 《弦长与直径的关系》

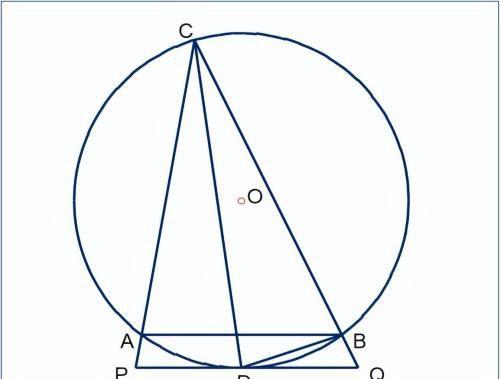
如图，△ABC内接于圆○，CD平分∠ACB交圆于点D，过D作PQ∥AB分别交CA、CB延长线于P、Q，连接BD；若AC、BQ的长是关于x的方程x＋4/x＝m的两个实数根，且tan∠PCD＝1/3；求圆○的半径。

〖一般性提点〗

圆周角一定时，该圆周角所对的弦长和圆半径R成正比。

给定圆周角的正切值，等于给定了该圆周角所对弦与直径的关系。

只要求出已知圆周角所对弦长，等同于求到半径。

详细参考题目分析。

〖题目分析〗

[1]. 角度/线段分析

<1>. ∠ACB的平分线CD，平分弦AB所对的弧，因此AD＝BD＝λ；

<2>. 由tan∠ACD＝1/3；在Rt△ADC1中：

得AD(及BD)与直径（2R）的关系：

λ＝2R/√10

<3>. 于是寻到一组三角形：△BDQ和△ACD，包含了题设的线段AC、BQ、以及与R存在定比关系的线段AD、BD。

[2]. △BDQ和△ACD相似：

由角平分线、线段平行、弦切角、圆周角诸信息，很容易证明

△BDQ∽△ACD，由此得：

AD·BD＝AC·BQ ①

[3]. 由题设，AC、BQ对应x＋4/x＝m的两个实数解：

x²－m·x＋4＝0

由韦达立定：

AC·BQ＝4；代入得①：

2R/√10＝√(AC·BQ)＝2；

∴ R＝√10。

本文内容由小娴整理编辑！