翻折题型找到每一个隐藏条件就没有解答的题(翻折问题)

导语：翻折题型：找到每一个隐藏条件，就没有解答不了的题目

宁可累，也别闲，宁可无，也别贪，人这辈子，忙碌才能充实自己，播种才能有所收获。苦过之后是甘甜，累到极致是蜕变。向所有拼搏中咬牙坚持的人致敬！

翻折类型的题目，往往隐藏很多条件，比如角相等，线段相等，线段垂直等等，一一准确找出来，解答相关类型的几何题简直不要太简单。请看下面这道题。

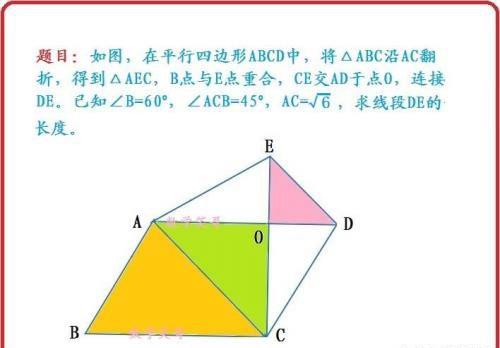
题目：如图，在平行四边形ABCD中，将△ABC沿AC翻折，得到△AEC，B点与E点重合，CE交AD于点O，连接DE。已知∠B=60°，∠ACB=45°，AC=，求线段DE的长度。

看似条件比较少，但已知条件结合翻折的特点，我们会得出比较多的隐藏条件，在解答题目中起到奇效。请看解答过程。

解：

①∵∠B=60°，∠ACB=45°，∴∠BAC=∠EAC=75°，∠ACE=∠ACB=45°，

∴∠BCE=90°。

又AD∥BC，∴CE⊥AD于O，∠OAC=∠ACB=∠OCA=45°。

②在平行四边形ABCD中，又∠B=60°，∠ACB=45°，∴∠BCD=120°，∠ACD=75°。

由翻折的特点可知，AE=AB=CD，

又∠EAC=∠ACD=75°，

∴四边形ACDE为等腰梯形，DE∥AC。

③∵∠OAE=∠EAC-∠OAC=75°-45°=30°，

∴在RT△OAE中，。

④根据等腰梯形的特点，△OAC∽△ODE，OA=OC

∴,

∴。

总结：

根据翻折的特点，我们找出了很多隐藏条件，轻松解答了题目。甚至我们还可以进一步解答出等腰梯形ACDE的面积，解答出平行四边形ABCD的面积。

朋友们还有什么好的思路和想法呢。

本文内容由小樊整理编辑！