垂直能得到什么条件(垂直问题)

导语：遇到多个垂直条件时垂心性质助你一马平川 - 初中联赛几何100题之14

本专题我们精选了初中数学联赛几何类题目一共100题，非常适合日常的练习，拓展思维。如果你成功完成了这套题，那想必你的几何功力会极大提升，也非常欢迎各位题友参与讨论，分享你的精彩解法。

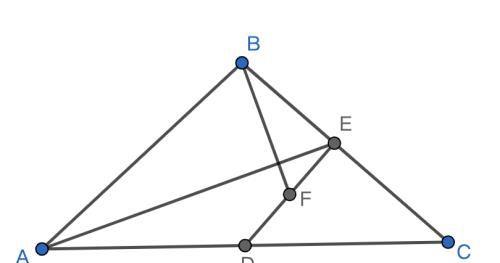
题目：已知：ABC 中，AB =BC ，D 是 AC 的中点，过 D 作 DEBC 于 E ，连接 AE ，取 DE中点 F ，连接 BF .

求证： AEBF .

如果你想思考一下，可以暂停滚屏，思考1分钟后，再继续。

题目分析：

观察特征，等腰，中点，连接BD后就有三线合一，

题目就变成已知两垂直，求第三条垂直线。

立刻联想到垂心，可以尝试从这个方向探索。

解法一：

已有的垂直条件不在一个三角形上，先通过辅助线集中在一起：

作DG//AE交AC于G，结论转化为,加上

知道F应该是的垂心。

所以,这意味着FG//CD

而从已知条件DG//AE，以及AD=CD，可以推导出EG=CG

加上DF=EF的条件，可以得到FG//CD。 已知条件和结论会师。

解法二：从结论倒推，从垂直成直角出发，发现相似三角形

假设结论成立，从图上可以看出，角a=角b，而直角三角形BCD斜边上的高DE分出了两个相似三角形，角c=角d

所以结论转化为求证

除了已知c=d外，只能求助于对应边成比例了。

观察等式

其中，DE=2DF，AC=2CD

等式化为

这个式子可以直接从推出。

已知条件和结论会师。

总结：遇到多个垂直条件，考虑垂心的判定和性质是一条路子；直角三角形内的相似模型，应该了然于心。

你做对了吗？如果你有更好的方法，欢迎分享。

【卡拉数学】长期分享数学趣题、解题技巧，致力于数学科普和拓展数学思维，每日定更，觉得内容有兴趣的可以长期关注哦！

本文内容由小茹整理编辑！