描述性统计分析的概念(描述性统计含义)
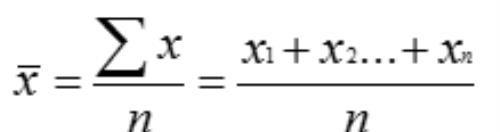
导语:描述性统计分析 之 概念简介
在实际工作中,我们都喜欢看到汇总好的数据,直观的数据,而不是未统计好的一堆数据,呈现数据方式有多种,最基础的就是数据的简单描述,也称之为描述性统计。
任何事物都有两面性,就像我们评价一个人、一个公司一样,从正反两个方面进行评价,数据的描述也是一样,有“集中”与“离散”两种趋势。
1. 集中趋势(1) 算数均数,简称均数(mean)
最常用来描述数据分布的集中趋势的统计指标,即描述一组数据在数量上的平均水平。总体均数用μ表示,样本均数用 表示。其计算公式是:
但均数不适用于对严重偏态分布的变量进行描述,也就是说,均数容易受到极端值的影响。由此,我们通常会用到下一个概念。
(2) 截尾均数
在进行均数描述时,若存在极端值,可考虑按照一定的比例去掉最两端的数据,然后再计算均数,因此,称之为截尾均数。若截尾均数与原均数相差不大,则说明数据不存在极值,或者两端的极值影响正好抵消。
常用的截尾均值是5%截尾均数,即两端各去掉5%的数据。
(3) 中位数 Median
顾名思义,就是中位数就是中间的数,那怎么算是中间的数?前提条件是将一组数据按照从小到大顺序排列,居于中间的数,即为中位数,它把全部数值分成两部分,比它小和比它大的数值个数正好相等。具体而言:
当n为奇数时,M=X(n+1)/2,当n为偶数时,M=(Xn/2+Xn/2+1)/2由于中位数是位置平均数,因此不受极端值的影响,在具有个别极大值或极小值的分布数列中,中位数比平均数更具代表性,代表数据的集中趋势。中位数适用于任意分布类型的资料,不过,由于中位数只考虑居中的位置,对信息的利用不充分。因此,对于对称分布的数据,可优先考虑使用均数,只用均数不能使用时,才考虑用中位数代替。(4) 众数
一组数据中,出现频次最多的数,即为众数,它也不受极端值的影响,但缺乏明确的统计特性,较少使用该指标。
2. 离散趋势(1) 全局 Range
全距又称为极差,是一组数据中最大值与最小值之差,是最为简单的变异指标,只能用于预备性检查。
(2) 分位数
通常,分位数用的比较多的是百分位数、四分位数、四分位数间距。
何谓百分位数?百分位数(Percentile)是一种位置指标,用Px标志,一个百分位数Px将一组数据分为两部分,理论上有x%的样本比它小,有(100-x)%的样本比它大。中位数就是一个特定的百分位数,即P50。
四分位数,就是P25,P50,和P75分位数的总称,三个分位数将所有数据等分为4部分。四分位数间距,也就是P75与P25的间距,它剔除了两端极值的影响。
(3) 方差和标准差
方差与标准差是表现数据 离散程度 的重要指标。
对于每个数据而已,离散程度的大小就是和均数的差值,简称为离均差,而 总体方差就是用离均差的平方除以样本n(见公式一)。
对于样本数据而已,方差的计算公式略有不同,差别在于是 离均差的评分除以样本n-1(见公式二),其中n-1也称之为自由度。
方差这个指标考虑了每个数据的离散趋势,消除了负号以及样本量的影响,确实已经不错了,可是也有缺点:因为采用平方去除负号,导致离散趋势被夸大;另一个是量纲不合常理。因此,提出了标准差。
标准差就是方差的平方根,即为:
由于标准差与方差计算涉及每一个变量值,虽然他们两个是最理想、最可靠的变异指标,但也会受到极端值的影响。实际上,方差和标准差的适用范围最好是服从正态分布的数据。
(4) 变异系数
有时在实际工作分析中,我们会比较不同度量单位的数据、不同量纲的数据,采用方差和标准差比较数据离散度就不太合适。如某班级学生身高数据均值为160.0cm,标准差为5.0cm,体重数据均值为50kg,标准差为4.0kg,请问身高和体重数据离散性哪个大呢?此时单位cm和kg是没法比的。
所以统计学家们提出了新的指标—变异系数,即用 各自离散趋势标准差除以各自的均数,由此,可消除了量纲的影响,比较离散程度就客观了。
3. 分布特征在自然界中,任何数据都有属于自己的分布,正态分布、二项式分布……。每一种分布都有描述数据的分布特征,所用的描述也略有不同,在本次,我们主要介绍正态分布的相关指标:偏度系数、峰度系数。
(1) 偏度Skewness
偏度是用来描述变量取值分布形态的统计量,指分布不对称的方向和程度(即为g1),是与正态分布相比而言的统计量。
g1<0 为负偏或左偏,长尾在左,峰尖偏右g1>0 为正偏或右偏,长尾在右,峰尖偏左g1=0 为对称分布,即正态分布(2) 峰度Kurtosis
峰度是用来描述变量取值分布形态陡缓程度的统计量(记为g2),指分布图形的尖峭程度或峰凸程度。峰度也相对于正态分布而言。
g2<0 为形态比较 平缓g2>0 为峰的形状 比较尖g2=0 为 正态峰本文内容由小岑整理编辑!