关于有理数的疑惑问题(有理数的收获与困惑)
导语:有理数学习中的几点困惑
在初一的数学学习中,学习到有理数这个概念,课本上介绍到整数和分数统称为有理数。很多学生在学习到这个概念的时候,就会有这样的疑问,什么是有理数?为什么要把整数和分数成为有理数呢?这个概念是从何而来的。
数的由来和发展
先说说有理数的发展,我们知道数学的每一次发展都是一次数系扩充的过程,随着生活及研究的需要,人们发现之前的数不够用了,于是就会对数系进行扩展,有理数就是这样产生的。
数的产生和发展离不开生活和生产的需要比如在远古时代为了计数牲畜的买卖量,往往采取用绳打结的方式计数,极其地不方便交易。
人们由于为了记数排序的方便、比较量的大小情况。产生类似于 1、2、3…这样的的自然数(正整数),并且随着古人们交易奴人和牲畜数量不断增加,记数时就不得不由个位逐渐向十位、百位、千位这样无限制地拓展。可以说数其实在人类社会初期并没有产生,即使产生了记数时用到的位数并不多也不大,但是随着生产以及生活实际的需要不得不拓展自然数的位数,可见数的产生和发展是与我们人类社会产生与发展密不可分的。
又比如由于在实际生活中为了表示“没有”“空位”,就产生了数“0”,也意思是说当我们用“0”这个数来表示存在与否的时候,代表的意思就是“空位”、“不存在”的意恩,当我们用“0”这个数表示数量上的情況,代表的意思就是“没有”的意思。
接着我们来看“9”和“10”,当古人计数数到了 9后就遇到了麻烦,因此为了突破计数上的束缚,于是古人在生活生产实践中就约定俗成数了“9”就进位开始数“10”,毕竟“10” 这个数字比“9”多一位数字“0”,认为他就比“9”大“1”,那么数了10后又数几呢?
那就数“11”,因为我们单个数时数了“0”后就紧挨着的是“1”,所以依此类推就该是用“12”“13”“14”……计数了.那由此可发现“0” 在我们生活计数实践中少了真还不行,数的进位也就无法有效进行。
那么分数的产生又是如何地呢?首先我们来了解人类历史,特別在原始社会时期,由于个人力量无法和大自然抗衡,原始的居民大家必须一起捕猎狩猎才能捕获大型的凶猛的哺乳野生动物,不这样他们食物来源就很难保障生存下去就会很困难。然而打猎的食物大家都得分享就必须合理分配;接着我们来看远古氏族社会分物时遇到的因惑,当某位氏族首领要给他们的下一代分田分屋分担财物时,不得不把他们的财物分担均匀,否则就会在他们儿孙子民中间产生怨气和矛盾甚至引起纷争,由于人类历史演变的需妥由此渐渐地产生了分数。
除了生活和生产中的需要,数学研究也是推动数系扩展的一个重要因素,古代埃及人约于公元前17世纪已使用分数,中国《九章算术》中也记载有分数的各种运算。分数的使用是由于除法运算的需要。除法运算可以看作求解方程px=q(p≠0),如果p、q是整数,则方程不一定有整数解,为了使方程有解,就必须把整数系扩大成为有理数系。
有理数这个概念是一个漂洋过海而来的错误翻译
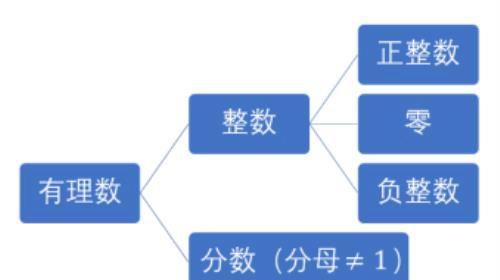
有理数,是整数和分数的统称,而整数又可以分为正整数、负整数和零。光看这个概念,很多同学还是一头雾水,因为这个概念并不能体现出有理数的特征。我们从有理数的本质去分析和理解。
数学上,有理数是一个整数a和一个非零整数b的比,通常这作a/b,故又称作分数。
因此有理数就是能够化为两个整数之比的数,有理数这个词来源于古希腊,其英文词根为ratio,就是比率的意思。有理数在英语中的全名为rational number,直译成汉语应该是“可比数。rational 通常的意义是“理性的”。
那么,为什么如今我们学习的名称不是“可比数”,而是“有理数”呢?这是由于数学知识在飘洋过海的过程中出现了“误读”,这是东西方数学文化传播中的一个著名乌龙事件。
有理数这一概念最早源自西方《几何原本》,在中国明代,从西方传入中国,明末数学家徐光启和学者利玛窦翻译《几何原本》前6卷时的底本是拉丁文。他们将这个词译为“理”,这里的“理”指的是它的本意“比值”。
而日本在明治维新以前,欧美数学典籍的译本多半采用中国文言文的译本。因此日本学者将中国文言文中的“理”直接翻译成了“道理”,而不是文言文所解释的“比值”,后来,日本学者直接用错误的理解翻译出了“有理数”和“无理数”。
在明治维新之后,日本的数学得到了迅猛的发展,到了清末,近代处于落后地位的中国不得不开始派遣留学生到日本进行学习,中国留学生又将错误传回中国,以至现在中日两国都用“有理数”和“无理数”的说法,于是“有理数”以讹传讹,沿用至今。
有理数的分类
根据有理数的概念,我们整数和分数统称为有理数,很多初学者不免会有这样的疑惑,我们之前所熟悉的小数该如何归类呢?小数究竟属不属于有理数呢?
首先来看看小数分分类:
按照小数部分分,根据小数位是否有限,可分为有限小数和无限小数,无限小数又分为无限循环小数和无限不循环小数。
根据我们之前所学的,根据小数的意义有限小数和分数之间可以实现互化。
根据小数的意义先将小数化为分母是10,100,1000,……的的分数,原来是几位小数就在1后面写几个0作为分母,把原来的小数点去掉后的数字做分子,能约分的化简成最简分数。
举例说明:
那么无限小数和分数之间可以实现互化吗?
根据分数与除法的关系,先把分数改写成除法算式,分子相当于被除数,分母相当于除数,再用分子除以分母,计算出结果(除不尽时,可按要求保留一定的小数位数)。
我们发现,有的分数能化为有限小数,如1/2,3/4,2/5,7/8,13/20……
有的分数只化为无限循环小数,如1/3,5/6,2/7,4/9,7/12……
那么哪些分数能化为有限小数呢?
一个最简分数,如果分母中只含有质因数2和5,再无其他质因数,那么这个分数可以化成有限小数;否则就不能化成有小数,可以化为无限循环小数。
所有的分数都能化为小数,有些可以化为有限小数,有些可以化为无限循环小数,那么反过来,是不是所有的有限小数和无限循环小数都能化为分数呢?该如何来转化呢?
如何将,,,,,……这些无限循环小数该如何转化为分数呢?
1纯循环小数化为分数的方法:
纯循环小数的循环节有几位,就在分母上写几个9,以循环节做分子:
2混循环小数化为分数的方法:
混循环小数的循环节有几位,就在分母上写几个9,循环节之前有几位,就在后面再补几个0做分母,
用从小数点后面第一位开始到第一个循环位结束时的数字组成的数减去第一个循环节前面的数字组成的数做分子,
因为有限小数和无限循环小数都可以转化为分数,所在在初中数学中把有限小数和无限循环小数也称为分数,因此有限小数和无限循环小数也是有理数。至于小数中的无限不循环小数,它就是无理数。
本文内容由小冰整理编辑!