涉及电流计算的三个特殊模型是(涉及电流计算的三个特殊模型有哪些)

导语：涉及电流计算的三个特殊模型

【同步学习】

环形电流，微观表达式，溶液导电

电流的强弱程度用电流这个物理量表示。单位时间内通过导体横截面的电荷量越多，电流就越大。如果用 I 表示电流，Q表示在时间 t 内通过导体横截面的电荷量，则有I=Q/t。

电流的形成

除常规问题外，涉及电流的计算时，还经常遇到以下几个特殊模型。

1. “环形”等效电流模型

原子模型中电子绕原子核的匀速圆周运动，匀强磁场中粒子的匀速圆周运动，带电圆盘绕中心的匀速转动······这些电荷的运动都可等效为一个环形电流。计算等效电流时，常取一个周期内通过某横截面的电量分析。

【示例】安培提出了著名的分子电流假说，根据这一假说，电子绕核运动可等效为一环形电流．设电荷量为e的电子以速率v绕原子核沿顺时针方向做半径为r的匀速圆周运动，则该环形电流的大小为........，电流方向为........。

解析：电子做圆周运动的周期T＝2πr/v，每个周期通过某横截面的电量为e。由电流I＝e/T得：I＝ve/2πr

电流的方向与电子的运动方向相反，即沿逆时针方向．

2. “柱体” 微元电流模型

如图所示，设柱体微元的长度为L，横截面积为S，单位体积内的自由电荷数为n，每个自由电荷的电荷量为q，电荷定向移动的速率为v，则：

柱体微元中的总电荷量为：Q＝nLSq

电荷通过横截面的时间：t＝L/v

电流的微观表达式：I＝Q/t＝nqvS

【示例】如图所示，一根长为L、横截面积为S的金属棒，其材料的电阻率为ρ，棒内单位体积自由电子数为n，电子的质量为m、电荷量为e.在棒两端加上恒定的电压时，棒内产生电流，自由电子定向运动的平均速率为v，则金属棒内的电场强度多大?

解析：由电流的定义可知：

由欧姆定律和电阻定律可得：

又因为E＝U/L，所以金属棒内的电场强度E＝ρnev。

3. 溶液 “离子”导电模型

对电解液而言，内部的正离子和负离子都可以参与导电。若取溶液内某横截面分析，则一段时间内，既有正离子通过该截面，又有负离子反向通过该界面，由于两种离子形成电流的方向相同，所以电流I＝Q/t中的电量Q应等于两种离子电量的绝对值之和。

若取阳极或阴极分析，则一段时间内只有正离子到达阴极，或只有负离子到达阳极，所以电量Q应等于正离子的带电量或负离子的带电量。

【示例1】探测放射线的计数管工作时，因为射线使内部气体电离，在时间t内有n个二价正离子到达阴极，有2n个电子到达阳极,则计数器中的电流I=........。

解析：时间t内到达阳极的电子的电量为:Q=2ne

由电流的定义可知：I＝Q/t＝2ne/t.

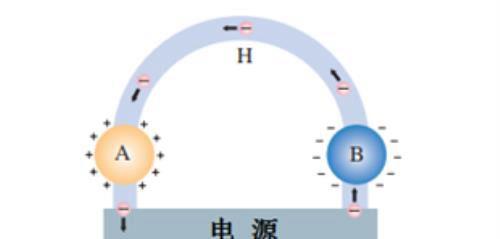
【示例2】如图所示，在NaCl溶液中，正、负电荷定向移动，方向如图中所示。若测得2s内分别有1×10^18个Na+和Cl-通过溶液内部的横截面M，试问:溶液中的电流方向如何?电流有多大?

解析：NaCl溶液中的Na+和Cl-在静电力作用下向相反方向定向移动形成电流，电流的方向与Na+定向移动的方向相同，即由指向.

Na+和Cl-都是一价离子,每个离子的电荷量为：q=1.6×10^-19C，NaCl溶液导电时, Cl-形成的等效电流方向与 Na+相同，所以溶液中的电流大小为:

根据以上信息还可以推知：2s内应有2×10^18个Na+到达阴极，或2×10^18个Cl-到达阳极，根据“示例1”的方法，同样可确定电流的大小。

【未经允许 请勿转载】

本文内容由小姬整理编辑！