数学解题反思怎么写(数学学累了怎么办)

“这道题老师讲了多少遍?为什么还是错?”
“这道题不是刚讲过吗?”
“这道题,我说过肯定会考,但还是很多同学没考起来。”
..............等等这些话语是很多学生耳熟能详的数学老师经典语录。
这些话看似教师的“恨铁不成钢”,其实代表一种数学学习方法。我们在换位思考一下,很多学生在数学学习过程中,做了大量题目,但是经常也会遇到这样的困惑:为什么同样的题目,我还是做错了?或是某道题目方法明明去记过,为什么这次考试没有想起来?等等这些情况,都说明了我们的学习方法出了问题。
无论一份中考数学试卷,还是高考数学试卷,大部分情况下都只有二十几个题目,我们不要说三年时间,单单在中考、高考最后一年做掉题目最少最少也上千个题,有些学生多起来就没上限。其实做了这么题目,毫不夸张地说中高考里面题型已经训练到,按道理应该都可以考到高分,但为什么最终分数总是那么差强人意呢?
如果数学学习,任何题目只要做一遍就掌握,做一遍就会,那该多好!不过,理想是美好的,但现实总是残酷的,很多时候我们的数学学习,同一个类型题目需要不断地去训练,才能慢慢掌握。那有没有什么方法,可以让我们少训练几次,就快速掌握同一类题型呢?答案肯定是有的,就在于解题反思、总结反思。

很多人可以检查一下自己的学习行为,每做完一道题目,你会不会认真去反思解题过程?反思这道题目用了哪些方法?反思解题步骤,每一步是不是都有理有据?反思解题过程中知识与结论是怎么联系上的等等。
我想很少有学生能到这一点,因为更多的人是做一题扔一题,一味的跳进题海,为解题而解题,满足题目做对即可,期望通过“题海战术”等等来取得数学学习的进步。往往这种方法到头来常常是事倍功半,对数学学习有作用,但不是很明显。
如果一个人在数学学习过程中,无法从解题训练进行解题反思、总结反思,缺乏对自身解题的认知过程进行反思,那么就很难获得数学学习启示,难以获得题目已有信息之外的更多有意义信息,从而最终降低了解题的收益率。
毫不夸张地说,绝大部分学生在解题的过程中只顾做题,对审题和解题反思、总结反思根本不重视。
在数学学习过程中,解题反思、总结反思是不可缺少的一环,但许多学生都没有真正意识到其重要性。实际上,获得问题的一个解答结果与对问题解答过程进行反思的差别,就像学习从“学会”到“会学”的转变。
数学联系实际生活、服务于生活,这是数学存在意义之一。如果学生在数学过程中只单纯在乎数学知识本身,只在乎答案正确与否,而不去考虑问题本身的意义,不去考虑题目的出题思路,那么同样的题型重新出现也是很容易出错。

有句名言“数学问题的解决仅仅只是一半,更重要的是解题之后的总结反思”。解题反思是对整个解题过程的反思,包括对题干理解的反思、习题涉及知识点的反思、解题思维程序的反思、解题结果表述的反思、解题所用方法规律和技巧的反思以及解题失误的反思等。
典型例题分析:
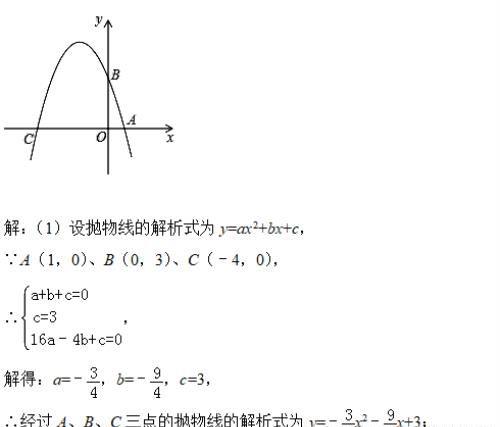
已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.


题干分析:
(1)设抛物线的解析式为y=ax2+bx+c,把A,B,C三点坐标代入求出a,b,c的值,即可确定出所求抛物线解析式;
(2)在平面直角坐标系xOy中存在一点P,使得以点A、B、C、P为顶点的四边形为菱形,理由为:根据OA,OB,OC的长,利用勾股定理求出BC与AC的长相等,只有当BP与AC平行且相等时,四边形ACBP为菱形,可得出BP的长,由OB的长确定出P的纵坐标,确定出P坐标,当点P在第二、三象限时,以点A、B、C、P为顶点的四边形只能是平行四边形,不是菱形;
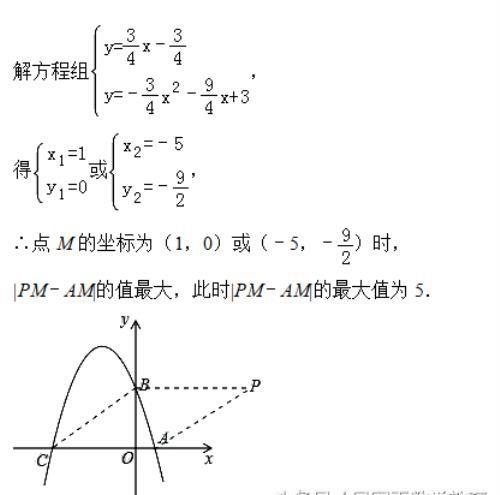
(3)利用待定系数法确定出直线PA解析式,当点M与点P、A不在同一直线上时,根据三角形的三边关系|PM﹣AM|<PA,当点M与点P、A在同一直线上时,|PM﹣AM|=PA,
当点M与点P、A在同一直线上时,|PM﹣AM|的值最大,即点M为直线PA与抛物线的交点,联立直线AP与抛物线解析式,求出当|PM﹣AM|的最大值时M坐标,确定出|PM﹣AM|的最大值即可。
解题反思:
此题属于二次函数综合题,涉及的知识有:二次函数的性质,待定系数法确定抛物线解析式、一次函数解析式,菱形的判定,以及坐标与图形性质,熟练掌握待定系数法是解本题的关键。

要想把一道题目做对,审题、搞清题意是解题的第一步,完全弄清题干所给条件,读懂、准确把握所给的问题,必要时还要适当画出图形,形成题目脉络,从而达到解题思路。这些,都属于解题反思的范畴,我们要好好记住。
数学学习,我们一定要学会思考,如题不会做,你是卡在哪一个步骤,为什么这个步骤是这么写,为什么用这个公式等等。
解题反思、总结反思我们更要关注知识的运用。如做完一道题,要思考知识点在题目当中是怎么呈现出来的,知识点与问题之间是怎么建立起联系,在解决问题过程,运用哪些数学思想方法等等。我们逐一去进行分析,去理清每一个细节,这样就会慢慢提高运用知识解决问题的能力。
解题反思不仅仅是对数学解题学习的一般性回顾或重复,而是深究数学解题活动中所涉及的知识、方法、思路、策略等,从中达到解决一类问题。
数学作为主要拉分科目之一,自然成为很多考生重点关注的对象。如果在数学学习过程中只会进行“题海战术”,不去把数学知识的条理脉络弄得清晰,形成知识网络,那么之后的学习就无法顺着数学脉络去走,造成数学学习脱节,无法抓住整个数学学习的节奏。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请与我联系,一经查实立刻删除内容。本文内容由快快网络小海创作整理编辑!