用正方形对角线怎么求面积(有正方形的对角线怎么求正方形的面积)

导语：应用正方形对角线上点的性质解题5例

应用正方形对角线上点的性质解题5例

我们知道，正方形既是轴对称图形，又是中心对称图形，其对角线上的任意一点到另一条对角线的两端点的距离相等，也就是说正方形中对角线上的点到另外两顶点的距离相等，由此形成的一些对称角度也相等。知晓这一性质，我们采用等量代换的技巧解决某些正方形相关问题，举例如下。

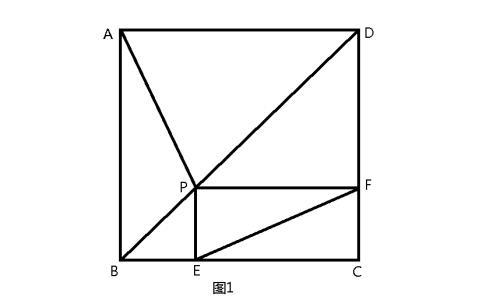
题目1：如图1，P是正方形ABCD对角线BD上一点，PE丄BC，PF丄DC。

求证：①AP=EF;②AP 丄EF。

解题思路：①本题要求正方形对角线上P点到一个顶点的距离（PA）等于另一条线段的长，我们可以联想到正方形中对角线上的点到另外两顶点的距离相等这一特征，自然想到连接PC（图2）。四边形PECF为矩形，其对角线 EF = PC，AP = PC，故AP = EF。

②过P点作 EF的平行线交DC于M，四边形 PEFM为平行四边形，AP = PC=EF= PM，∠PCM =∠PMC =∠PAD = a。

∠PMC + ∠ PMD = 180°，∠PMD + ∠ PAD = 180°。故∠APM = 360°-∠ADM-∠PMD-∠PAD = 360°-90°-180°= 90°(证明四点共圆亦有解)，故AP丄PM，AP丄EF成立。

题目2：如图，过正方形ABCD的顶点A作直线交BD于E，交CD于F，交BC的延长线于G。若H是FG的中点，求证：EC⊥CH。

解题思路：根据正方形中对角线上的点到另外两顶点的距离相等，由此形成的一些对称角度也相等；平行线性质及直角三角形斜边中线性质得出图中一些角度相等，EC⊥CH可快速得到证明。

题目3：图1，G是正方形ABCD的边DC上一点，连接AG并延长交BC延长线于K，求证1/2（AG+AK）＞AC。

解题思路：连接BD交AC于O，交AK于M；取GK中点N，连接CN、CM。

根据题目2证明△MCN为直角三角形，斜边MN＞MC。

直角三角形MOC中，斜边MC＞OC，同样，MA＞OA，

即AN＞AC。

1/2（AG+AK）=1/2（AG+AG+GK）

=1/2（2AG+2GN）。

1/2（AG+AK）=AN。

1/2（AG+AK）＞AC成立。

题目4：如图，正方形ABCD中，过点D作DP交AC于点M、交AB于点N，交CB的延长线于点P，若MN=1， PN=3，则DM的长为（2）。

解题思路：本题求一条直线上三条线段之间的关系，应想法转变成稍复杂的图形关系来解题。连接MB，MB等量替换为MD，即MB=MD（图2），

∠ADM=∠ABM=∠DPC=α。

△MNB∽△MBP

MB/MP=MN/MB（母子相似三角形）

MB²=MN·MP=4

MB=MD=2。

题目5：在正方形 ABCD 中，F为CD上一点，G 为对角线BD上一点，FG⊥BD,M为BG 中点，连接 AM、MF。求证：AM=MF, AM⊥MF。

解题思路：本题类似题目1，请参考之（图2）。

本文内容由小萱整理编辑！